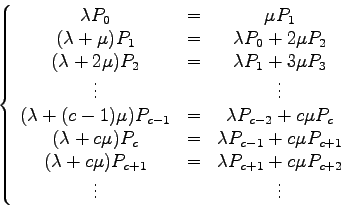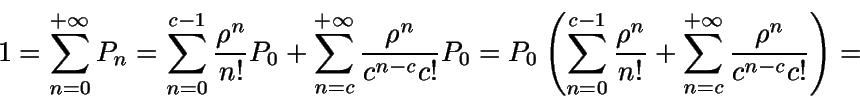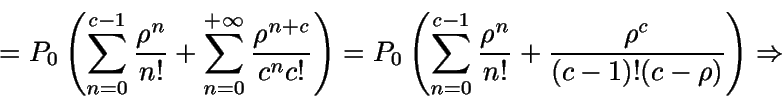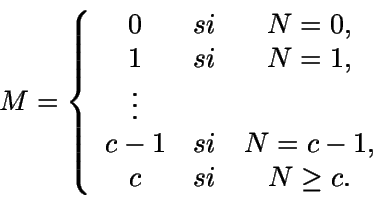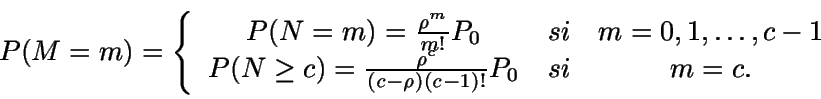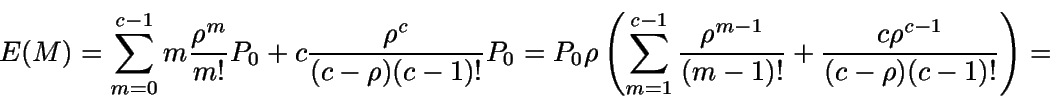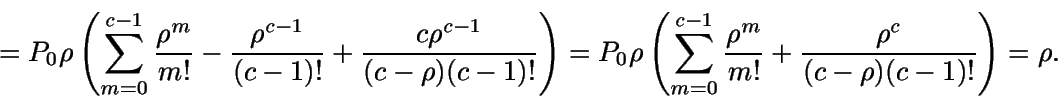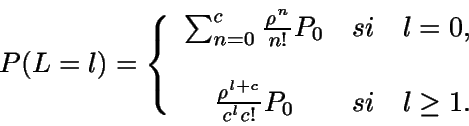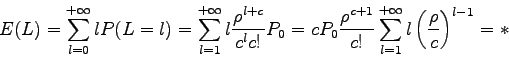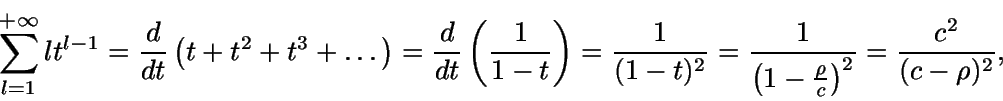Modelo M/M/c

Se tiene una única cola a la que se llega según un proceso de Poisson de parámetro 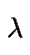$\lambda$.

Los c servidores trabajan independientemente, pero todos con tiempo de servicio Exp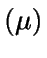$(\mu)$.

Se sabe que existe el estado estacionario si, y sólo si, se cumple

$$\frac{\lambda}{\mu c} < 1.$$

De nuevo, definimos $\rho = \frac {\lambda}{\mu}$.

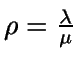Para cada servidor ocupado se tiene

$$P(\text{finalizar un servicio en }[t,t+h])=\mu h + o(h).$$

Entonces

$$P(\text{finalizar un servicio entre todos los servidores en } [t,t+h])=c \mu h + (h).$$

Así, si hay n clientes en el sistema, 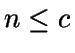$n \leq c$,

$$P(\text{una salida})= n\mu h + o(h).$$

Con 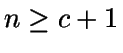$n\geq c+1$ clientes en el sistema:

$$P(\text{una salida})=c\mu h + o(h).$$

El diagrama de flujos asociado es el siguiente:

Las ecuaciones que se obtienen son:

$$\left \{ \begin{array}{ccc} \lambda P_0 & = & \mu P_1 \\ (\... ...+1} + c \mu P_{c+2} \\ \vdots & & \vdots \end{array} \right.$$

Por su estructura, este sistema puede resolverse de forma descendente. Resolviendo la primera ecuación:

$$P_1 = \rho P_0.$$

Si ahora sustituimos en la segunda:

$$(1+\rho)\rho P_0 = \rho P_0 + 2P_2\Rightarrow$$

$$P_2 = \frac{\rho^2}{2} P_0.$$

En general, se tiene

$$P_n = \left \{ \begin {array}{ccc} \frac{\rho^n}{n!} P_0 & ,&... ...ac{\rho^n}{c^{n-c} c!} P_0 & , & n \geq c. \end{array} \right.$$

Teniendo ahora en cuenta que la suma de las probabilidades debe ser uno y que 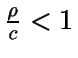$\frac {\rho}{c} < 1$ podemos calcular P₀:

$$1=\sum_{n=0}^{+\infty} P_n= \sum_{n=0}^{c-1} \frac{\rho^n}{n!... ...!} + \sum_{n=c}^{+\infty} \frac{\rho^n}{c^{n-c}c!} \right ) =$$

$$= P_0 \left ( \sum_{n=0}^{c-1} \frac{\rho^n}{n!} + \sum_{n=0}... ...rho^n}{n!} + \frac {\rho^c}{(c-1)!(c-\rho)} \right)\Rightarrow$$

$$P_0= \frac{1}{\sum_{n=0}^{c-1}\frac{\rho^n}{n!} + \frac {\rho^c} {(c-1)!(c-\rho)}}.$$

Número medio de servidores ocupados

Se define ahora la variable aleatoria M como el número de servidores ocupados en estado estacionario. Escribiendo M en función de N:

$$M=\left \{ \begin {array}{ccc} 0 & si & N=0, \\ 1 & si ... ...c-1 & si & N=c-1, \\ c & si & N\geq c. \end{array} \right.$$

Luego

$$P(M=m)= \left \{ \begin {array}{ccc} P(N=m) = \frac{\rho^m}{... ... {\rho^c}{(c-\rho)(c-1)!} P_0 & si & m=c. \end{array} \right.$$

Entonces, el número medio de servidores ocupados será

$$E(M)= \sum_{m=0}^{c-1} m \frac{\rho^m}{m!} P_0 + c \frac{\rh... ...{m-1}}{(m-1)!} + \frac{c\rho^{c-1}}{(c-\rho)(c-1)!} \right ) =$$

$$= P_0 \rho \left ( \sum_{m=0}^{c-1} \frac{\rho^m}{m!} - \fra... ...c{\rho^m}{m!} + \frac{\rho^c}{(c-\rho)(c-1)!} \right ) = \rho.$$

Número medio de clientes en cola

$$L=\left \{ \begin {array}{ccc} 0 & si & N=0,1,\dots,c \\ N-c & si & N\geq c+1. \end{array} \right.$$

Así

$$P(L=l)=\left \{ \begin{array}{ccc} \sum_{n=0}^c \frac{\rho^n}... ...c{\rho^{l+c}}{c^l c!} P_0 & si & l\geq 1. \end{array} \right.$$

Entonces

$$E(L)=\sum_{l=0}^{+\infty} l P(L=l) = \sum_{l=1}^{+\infty} l ... ...sum_{l=1}^{+\infty} l \left ( \frac{\rho}{c} \right )^{l-1} = *$$

Haciendo ahora 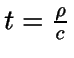$t=\frac{\rho}{c}$ se tiene

$$\sum_{l=1}^{+\infty} l t^{l-1} = \frac {d}{dt} \left ( t + t... ...\left ( 1-\frac{\rho}{c} \right)^2} = \frac {c^2}{(c-\rho)^2},$$

por lo que

$$*=\frac{\rho^{c+1}}{c c!} \frac {c^2}{(c-\rho)^2} P_0 = \frac {\rho^{c+1}}{(c-1)! (c-\rho)^2} P_0.$$