



Siguiente: Métodos específicos de generación de vv.aa.
Nivel anterior: Métodos generales de generación de vv.aa.
Previa: Método de composición
Sea
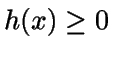 tal que
tal que
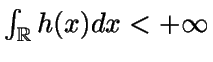 , y sea
, y sea
Se cumple:
- 1.
- C(h) tiene área finita.
- 2.
- Si (U,V) sigue una distribución uniforme en C(h), entonces la
función de densidad de
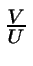 es
es
Demostración:
(i) Se define
Entonces el área de C(h) es
(ii)
(La igualdad en el
último paso es consecuencia de que tanto fX como h son
funciones de densidad)
Ejemplo:
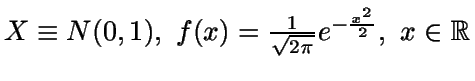 .
Tomemos
.
Tomemos
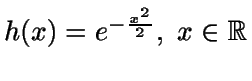 .
.
Acotación de u:
Luego
 .
.
Acotación de v:
(Esto último se debe a que
![$u\in [0,1]$](img491.gif) y el máximo se alcanza en
y el máximo se alcanza en
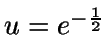 )
)
Así se tiene el siguiente algoritmo:
- 1.
- Se genera u1,
 e independientes.
e independientes.
- 2.
- Sea
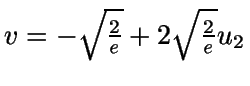 .
.
- 3.
- Si
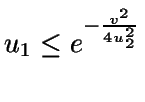 ,
entonces se toma
,
entonces se toma
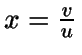 .
En caso contrario se repite el paso 1.
.
En caso contrario se repite el paso 1.

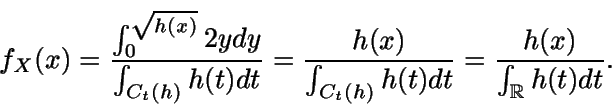
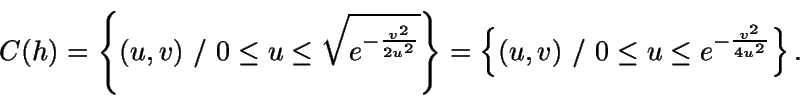
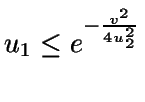 ,
entonces se toma
,
entonces se toma