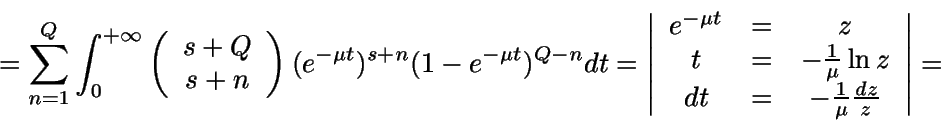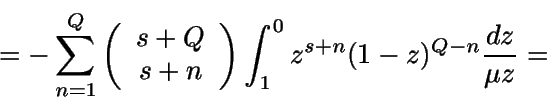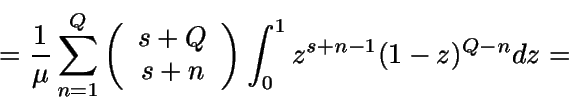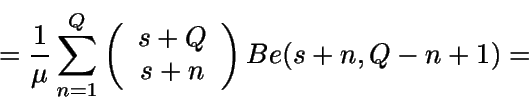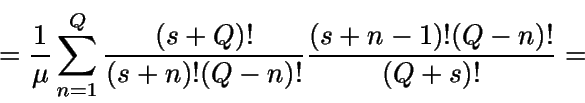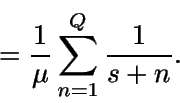Siguiente: Modelos de inventario con revisión periódica
Nivel anterior: Modelos de inventario con revisión continua
Previa: Modelo 5
- El inventario es discreto.
- Escasez prohibida.
- Coste material constante.
- Coste de pedido k.
- Coste de mantenimiento h.
- Demanda: la probabilidad de que una unidad concreta de porducto
sea demandada en el período de tiempo [t,t+dt] es
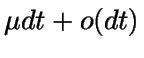 .
El que se demande un objeto es independiente de que se
demande cualquier otro. La probabilidad de hacer dos pedidos en
[t,t+dt] es o(dt).
.
El que se demande un objeto es independiente de que se
demande cualquier otro. La probabilidad de hacer dos pedidos en
[t,t+dt] es o(dt).
- Política: cuando el nivel de inventario desciende hasta s, se
piede Q y se eleva el nivel a s+Q=S.
En estado estacionario:
Sea Pj la probabilidad de que haya j objetos en el inventario
en estado estacionario.
(Como hay conservación de flujos, la ecuación del nodo s+Q,
es redundante)
Al resolver el sistema:
Ahora
Luego
Determinemos ahora el nivel medio de inventario en estado
estacionario:
Así que el coste de mantenimiento medio por unidad de tiempo en
estado estacionario es
Sin embargo, para el coste de pedido no tiene sentido trabajar con
el estado estacionario. Debemos usar el transitorio para saber la
longitud media de un período.
(El período va desde s+Q hasta s+1)
Sea Pn(t) la probabilidad de que haya n objetos en el
inventario en el instante t.
Si n<s+Q:
Si n=s+Q:
Resolviendo este sistema (hacia atrás):
Sea ahora Y la longitud de un período. Como
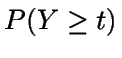 es la
probabilidad de que estemos en alguno de los estados s+1,...
, s+Q en el instante t, entonces
es la
probabilidad de que estemos en alguno de los estados s+1,...
, s+Q en el instante t, entonces
Así que
Coste de pedido:
Coste total:
Se busca
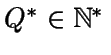 tal que
tal que

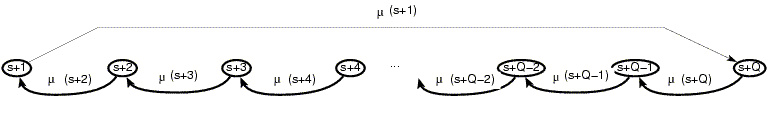
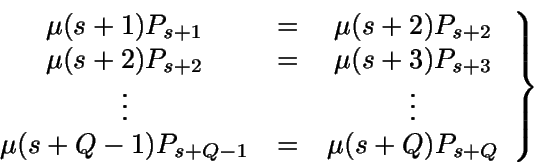
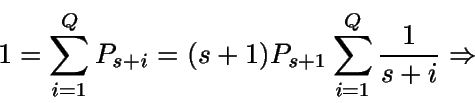
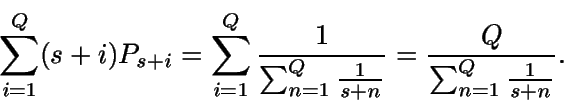
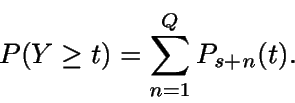
![\begin{displaymath}E[Y] = \int_0^{+\infty} {P(Y>t)} dt =
\sum_{n=1}^Q \int_0^{+\infty} {P_{s+n}(t)} dt = \end{displaymath}](img731.gif)