



Siguiente: Generación de variables continuas
Nivel anterior: Métodos específicos de generación de vv.aa.
Previa: Métodos específicos de generación de vv.aa.
Subsecciones
Sea X una variable aleatoria discreta con función de
distribución F y probabilidades puntuales
Considerando la función F, que es escalonada, se tiene el
siguiente algoritmo:
- 1.
- Se hace s=p1, i=1.
- 2.
-
- Se genera
 .
.
Si  ,
entonces x=xi es el valor que se genera y
finaliza el algoritmo.
Si u>s, entonces se hace i=i+1, s=s+pi y se repite el paso 2.
,
entonces x=xi es el valor que se genera y
finaliza el algoritmo.
Si u>s, entonces se hace i=i+1, s=s+pi y se repite el paso 2.
(Este método sólo es válido para variables cuya probabilidad está
concentrada en un número finito de puntos)
Sea X tal que
P(X=xi)=pi,
 .
Tras una fase de
preprocesamiento que se detalla más adelante, se tiene el
siguiente algoritmo:
.
Tras una fase de
preprocesamiento que se detalla más adelante, se tiene el
siguiente algoritmo:
- 1.
- Se genera
 .
Sean y=1+[ku],
z=frac(ku).
.
Sean y=1+[ku],
z=frac(ku).
- 2.
- Si
 ,
entonces k=y. Si z>Q(y), entonces k=A(y).
Se toma x=xk.
,
entonces k=y. Si z>Q(y), entonces k=A(y).
Se toma x=xk.
Falta determinar los valores Q(i) y los
alias A(i) de modo que se tenga
Fase de preprocesamiento:
- 1.
- Para cada
 se define
se define
- 2.
- Se repiten las siguientes operaciones (a lo sumo) k-1 veces:
- Selecciónese i tal que
 ,
Ii=true.
Si esto no es posible, finaliza el preprocesamiento.
,
Ii=true.
Si esto no es posible, finaliza el preprocesamiento.
- Selecciónese j tal que
 ,
Ij=true.
,
Ij=true.
- Hágase Ii=false, A(i)=j, Q(i)=kai,
 .
.
Ejemplo: Sea
 con x=0,1,2,3. El vector de probabilidades es
(
con x=0,1,2,3. El vector de probabilidades es
(
 )
)
i=4, j=1, I(4)=False, A(4)=1,
 ,
,

i=3, j=2, I(3)=False, A(3)=2,
 ,
,

i=1, j=2,
 ,
A(1)=2,
,
A(1)=2,

Ahora asignamos el 1 al valor 0, el 2 al 1, el 3 al 2 y el 4 al 3, con lo
cual cuando apliquemos la segunda parte del algoritmo del alias nos
dará los valores que buscamos.
Representa el número de fracasos hasta que se produce el primer
éxito en un experimento de Bernouilli de parámetro p.
La variable geométrica se puede relacionar fácilmente con la
variable exponencial:
Sea
 .
.
Sea x>0.
Como
 ,
tomemos
,
tomemos 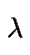 tal que
tal que
 para conseguir la expresión de probabilidad
puntual de una distribución G(p). Basta tomar
para conseguir la expresión de probabilidad
puntual de una distribución G(p). Basta tomar
 .
Tras esto se toma un valor y generado según una
.
Tras esto se toma un valor y generado según una
 y se toma x=[y]. Ya se vio que para ello hay
que hacer
y se toma x=[y]. Ya se vio que para ello hay
que hacer
 ,
con
,
con
 ,
por lo que se concluye que
,
por lo que se concluye que
Representa el número de fracasos antes del r-ésimo éxito en un
experimento de Bernouilli de parámetro p.
Existen varias formas de simular variables con distribución
binomial negativa: la más inmediata es ir simulando experimentos
de Bernouilli de parámetro p y contabilizar los fracasos hasta
que se obtiene el éxito r-ésimo. Otro modo consiste en observar
que una variable BN(p,r) es suma de r variables geométricas
G(p) independientes, por lo que basta simular r veces una
geométrica con parámetro p y sumar los valores obtenidos.
Veamos también un algoritmo directo basado en el método de composición.
Sean
 (Poisson) y
(Poisson) y
 .
.
Luego esta composición es
 .
Como nosotros queremos simular una BN(p,r), entonces
debemos tomar
.
Como nosotros queremos simular una BN(p,r), entonces
debemos tomar  ,
,
 ,
resultando el
siguiente algoritmo:
,
resultando el
siguiente algoritmo:
- 1.
- Se genera
 .
.
- 2.
- Se genera
 .
.
Este valor x está distribuido según una distribución binomial
negativa BN(p,r).
En la primera parte de la asignatura se vio que si los
tiempos entre sucesos consecutivos son
 ,
entonces
el número de sucesos por unidad de tiempo sigue una distribución
de Poisson de parámetro
,
entonces
el número de sucesos por unidad de tiempo sigue una distribución
de Poisson de parámetro 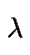 .
En consecuencia, para generar
una variable
.
En consecuencia, para generar
una variable
 ,
podemos proceder del siguiente modo: se
generan valores
,
podemos proceder del siguiente modo: se
generan valores
 tales que
tales que
 .
Ese valor x corresponderá a
una variable
.
Ese valor x corresponderá a
una variable
 .
.
Como los valores Tj son exponenciales de parámetro 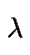 ,
entonces se tiene que
,
entonces se tiene que
 ,
con
,
con
 ,
por lo que
,
por lo que
En resumen, el algoritmo es el siguiente:
- 1.
- Sean k=1, x=1.
- 2.
- Se genera
 y se hace k=kui.
y se hace k=kui.
- 3.
- Si
 ,
entonces x-1 es el valor buscado. En
caso contrario se hace x=x+1 y se va al paso 2.
,
entonces x-1 es el valor buscado. En
caso contrario se hace x=x+1 y se va al paso 2.








