Caso práctico resuelto
Introducción
En muchas ocasiones para estudiar un fenómeno se dispone de gran cantidad de variables algunas de las cuales están correlacionadas entre sí, lo que complica su análisis. En estas situaciones es conveniente aplicar un método, como el de componentes principales, que permita reducir el número de variables sin pérdida sustancial de información, y consiguiendo que estas nuevas variables sean incorreladas evitando así que haya información redundante.
En este caso práctico vamos a reducir el número de variables económico-financieras que describen a un grupo de empresas murcianas dedicadas al transporte de mercancías por carretera, conservando el máximo de información posible. El punto de partida es la información económico-financiera del año 2016 de 459 empresas de la Región de Murcia de este sector (código CNAE 4941), extraída de la base de datos SABI. Para cada empresa se dispone de datos para las siguientes variables:
- apalanc: apalancamiento (%)
- capital: capital social (miles de euros)
- ebitda.ventas: ebitda sobre ventas (%)
- empleados: plantilla de la empresa (personas)
- fondos: fondos propios (miles de euros)
- ingresos: ingresos de explotación (miles de euros)
- reco: rentabilidad económica (%)
- rfin: rentabilidad financiera (%)
- res.ventas: resultado del ejercicio sobre ventas (%)
Datos del problema
La información relativa a las variables anteriores está recogida en el fichero datos.RData. Guarde los datos y cárguelos para comenzar:
load("datos.Rdata")y realice una visualización preliminar,
str(datos)## 'data.frame': 459 obs. of 9 variables:
## $ apalanc : num 14.6 246.3 25.7 47.1 550.3 ...
## $ capital : num 7240 12926 120 668 98 ...
## $ ebitda.ventas: num 10.56 10.69 8.05 4.26 6.55 ...
## $ empleados : num 224 611 236 94 712 404 41 188 32 26 ...
## $ fondos : num 84671 24159 17416 10035 3367 ...
## $ ingresos : num 330816 136077 96829 61660 58029 ...
## $ reco : num 25.49 6.47 11.45 4.51 2.87 ...
## $ rfin : num 40 32.1 28 16.1 22.5 ...
## $ res.ventas : num 8.188 4.42 3.758 2.01 0.775 ...Como se puede ver el objeto contiene 9 variables numéricas con rangos de variación diferentes.
Paso 1. Exploración de los datos
En primer lugar, se calculan los principales descriptivos para las variables. Para ello, una vez instalado el paquete pastecs con install.packages("pastecs"), se usa la función stat.desc incluida en dicho paquete. La sintasis pastecs::stat.desc, evita tener que cargar previamente el paquete con library, pero obliga a escribir el nombre del paquete seguido con :: cada vez que se use una función del mismo.
pastecs::stat.desc(datos, basic = F)## apalanc capital ebitda.ventas empleados
## median 9.458600e+01 4.700000e+01 9.1128245 6.000000
## mean 1.949645e+02 1.422505e+02 10.3395298 17.135076
## SE.mean 9.453865e+01 3.334973e+01 0.5895011 2.498188
## CI.mean.0.95 1.857833e+02 6.553745e+01 1.1584623 4.909332
## var 4.102338e+06 5.105017e+05 159.5078133 2864.593068
## std.dev 2.025423e+03 7.144940e+02 12.6296403 53.521893
## coef.var 1.038868e+01 5.022789e+00 1.2214908 3.123528
## fondos ingresos reco rfin res.ventas
## median 1.278163e+02 6.957005e+02 3.4490000 15.07700 1.9017594
## mean 7.921479e+02 3.512870e+03 4.4643704 33.92598 2.4175629
## SE.mean 2.033015e+02 8.481778e+02 0.6017126 18.89548 0.4027344
## CI.mean.0.95 3.995194e+02 1.666803e+03 1.1824597 37.13259 0.7914363
## var 1.897116e+07 3.302072e+08 166.1846244 163881.02480 74.4474907
## std.dev 4.355589e+03 1.817160e+04 12.8912616 404.82221 8.6282959
## coef.var 5.498454e+00 5.172866e+00 2.8875878 11.93251 3.5690058Se puede observar que hay grandes diferencias entre las varianzas de las variables, desde el 74.4474907 de res.ventas hasta el 3.302072e+08 de ingresos, lo que puede afectar a los resultados de un análisis de componentes principales (ACP), debido a que las variables con mayor varianza tendrán más influencia en la generación de un componente.
El ACP tiene sentido cuando hay correlación entre las variables pues permite eliminar información redundante. Si se analiza la matriz de correlaciones se puede ver, a modo de ejemplo, que hay correlaciones fuertes, tanto negativas, como la que existe entre el apalancamiento y el resultado financiero (-0.88), como positivas, como las que hay entre los fondos y los ingresos (0.97) o entre el ebitda sobre ventas y el resultado sobre ventas (0.83).
R <- cor(datos)
corrplot::corrplot(R, method = "number",
number.cex = 0.75) # Matriz de correlaciones con números en letra pequeña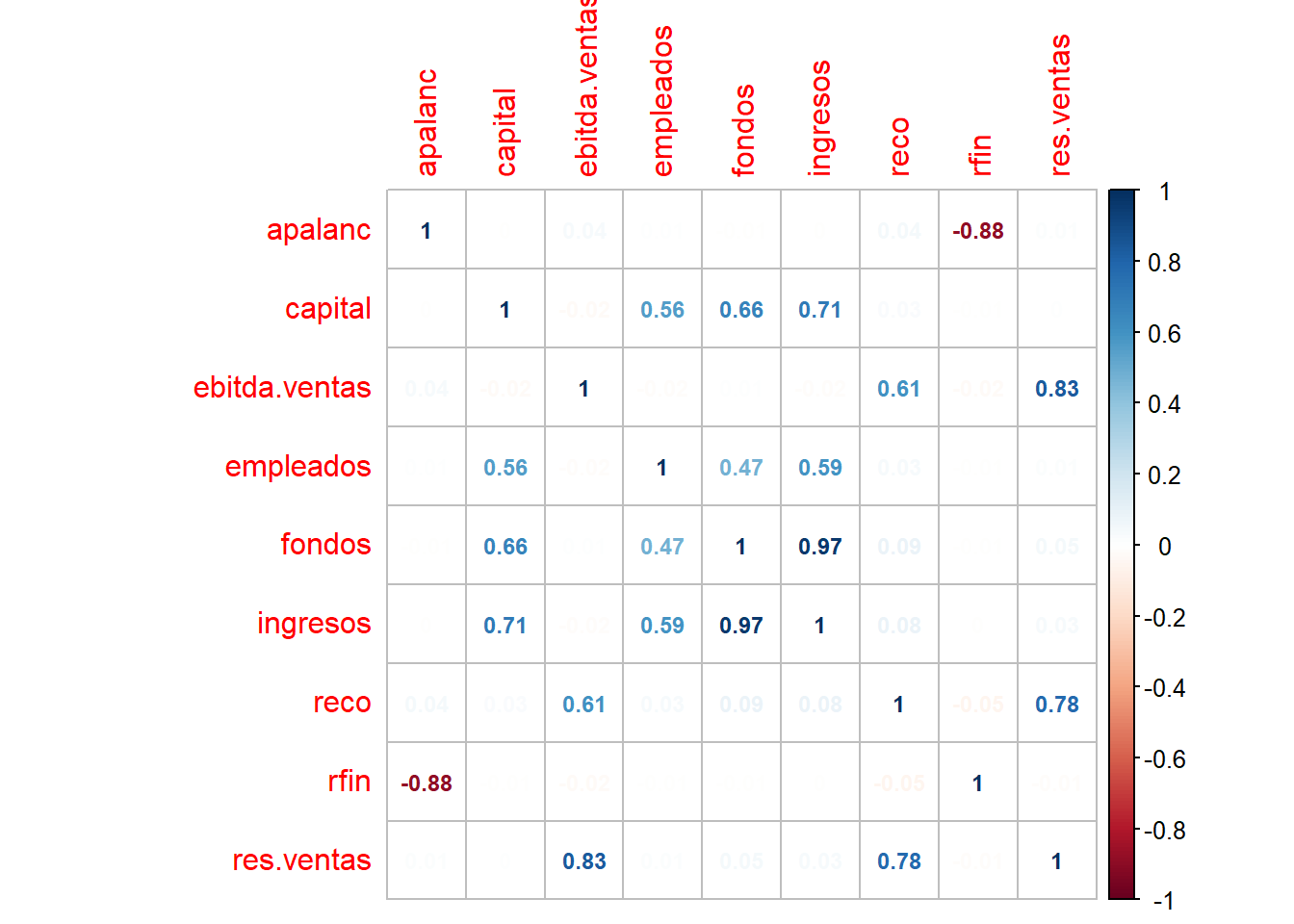
En las funciones de R que llevan a una salida gráfica existen con frecuencia argumentos que, sin ser necesarios, pueden mejorar el resultado final de manera muy efectiva. Es el ejemplo del argumento number.cex de la función anterior. En la elaboración de los gráficos en este documento se emplea este tipo de argumentos en numerosas ocasiones. En los casos en los que se ha considerado interesante resaltar su utilidad se ha empleado el argumento en una línea aparte, añadiendo un comentario.
Paso 2. Extracción de los componentes principales
Para la obtención de los componentes principales se puede utilizar la función princomp. Para evitar la influencia de la diferencia en magnitud de las varianzas se puede emplear los datos originales y el argumento cor = TRUE o los datos originales estandarizados y el argumento cor = FALSE. En ambos casos, la suma de las varianzas de las variables originales y la de los componentes coincidirá con el número de variables de la matriz de datos original.
princomp(datos, cor = TRUE)## Call:
## princomp(x = datos, cor = TRUE)
##
## Standard deviations:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
## 1.7377611 1.5748797 1.3695262 0.7767213 0.6328808 0.6031328 0.3478603
## Comp.8 Comp.9
## 0.3400504 0.1417537
##
## 9 variables and 459 observations.La salida de la función princomp puede guardarse en un objeto que contiene más información que la visualizada. Con summary no solo se ven las desviaciones típicas de los componentes, sino también el porcentaje de varianza total explicada por cada uno de ellos.
componentes <- princomp(datos, cor = TRUE)
summary(componentes)## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 1.7377611 1.5748797 1.3695262 0.77672134 0.63288079
## Proportion of Variance 0.3355348 0.2755829 0.2084002 0.06703289 0.04450423
## Cumulative Proportion 0.3355348 0.6111177 0.8195179 0.88655083 0.93105506
## Comp.6 Comp.7 Comp.8 Comp.9
## Standard deviation 0.6031328 0.3478603 0.34005041 0.141753692
## Proportion of Variance 0.0404188 0.0134452 0.01284825 0.002232679
## Cumulative Proportion 0.9714739 0.9849191 0.99776732 1.000000000Los componentes están ordenados en función de la varianza que explican y el porcentaje acumulado permite decidir con cuántos componentes trabajar. En este caso con solo dos se explica el 61.11%, con tres el 81.95% y con cuatro el 88.66%. El objeto creado ofrece más información, como se describe a continuación.
Componentes como combinación lineal de las variables
El objeto componentes contiene los coeficientes que permiten expresar cada uno de los componentes como combinación lineal de las variables originales estandarizadas. Esta información está recogida en $loadings:
componentes$loadings##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## apalanc 0.702 0.237 0.664
## capital 0.479 0.438 -0.750
## ebitda.ventas 0.562 0.567 0.305 0.462 -0.205
## empleados 0.415 0.840 -0.191 0.257
## fondos 0.524 -0.455 0.269
## ingresos 0.546 -0.275 -0.113 0.243
## reco 0.113 0.538 -0.653 -0.379 0.339
## rfin -0.702 0.263 0.655
## res.ventas 0.596 -0.739 0.274
## Comp.9
## apalanc
## capital
## ebitda.ventas
## empleados 0.115
## fondos 0.660
## ingresos -0.739
## reco
## rfin
## res.ventas
##
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## SS loadings 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000
## Proportion Var 0.111 0.111 0.111 0.111 0.111 0.111 0.111 0.111
## Cumulative Var 0.111 0.222 0.333 0.444 0.556 0.667 0.778 0.889
## Comp.9
## SS loadings 1.000
## Proportion Var 0.111
## Cumulative Var 1.000La salida anterior es útil a efectos de interpretación, pero se ocultan los coeficientes inferiores a 0.1 en valor absoluto. Si desea ver todos los coeficientes puede emplear:
componentes$loadings[ ,1:9]## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## apalanc 0.00655167 0.08475443 0.701693265 0.00451166 0.03212559
## capital 0.47912293 -0.09232221 0.004862422 0.08111504 0.43770776
## ebitda.ventas 0.06207123 0.56245352 -0.067324955 0.05288579 0.56734582
## empleados 0.41532340 -0.07629194 0.009402874 0.83986630 -0.19109492
## fondos 0.52358761 -0.06373829 -0.003191079 -0.45460454 -0.07067235
## ingresos 0.54613349 -0.07992855 0.001052963 -0.27499508 -0.11261109
## reco 0.11310163 0.53804853 -0.047726376 -0.04542996 -0.65266209
## rfin -0.01158476 -0.08269831 -0.702002522 0.01260367 0.01361748
## res.ventas 0.09338080 0.59609773 -0.088798740 0.02678373 0.07177909
## Comp.6 Comp.7 Comp.8 Comp.9
## apalanc 0.02978363 0.236982842 0.66401824 0.037145102
## capital -0.75043525 0.004197640 0.01119148 0.020748907
## ebitda.ventas 0.30502552 0.462248076 -0.20543903 -0.040783841
## empleados 0.25683680 0.007966801 -0.02155086 0.114942925
## fondos 0.26946841 0.008540688 -0.03921824 0.660226599
## ingresos 0.24330824 -0.011707222 0.04560329 -0.738667288
## reco -0.37919389 0.339318757 -0.09188864 0.005792861
## rfin 0.01975233 0.262989263 0.65503345 0.035392438
## res.ventas 0.03104641 -0.738629937 0.27414379 0.022356680Así, el primer componente vendría dado por la siguiente combinación lineal de las variables originales estandarizadas:
\[Comp.1 = 0.0066 \cdot z_{apalanc} +0.4791 \cdot z_{capital} +0.0621 \cdot z_{ebitda.ventas} +...- 0.0116 \cdot z_{rfin}+0.0934 \cdot z_{res.ventas}\]
donde el símbolo z indica que la variable está estandarizada. A partir de esta expresión se pueden obtener las puntuaciones de las empresas en este componente.
Puntuaciones de las empresas en los componentes
En el objeto componentes también están disponibles las puntuaciones de cada una de las observaciones (empresas) en el nuevo espacio formado por los componentes. A continuación mostramos las puntuaciones de 6 de ellas con la función head:
head(componentes$scores)## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## 1 26.560899 -2.6048220 -0.16950893 -9.7219520 -0.7899918 2.517655
## 2 20.037224 -3.1866039 0.17313469 6.3329265 4.4472656 -7.407665
## 3 6.557825 -0.6872858 -0.04424650 0.2543293 -2.0934164 3.096068
## 4 3.777499 -0.8692112 0.02985954 -0.6072561 -0.7457002 1.015876
## 5 7.269370 -1.5958065 0.30924872 9.8007803 -2.9888914 4.228950
## 6 6.242442 -1.6076261 0.17795085 3.9481944 -1.8129481 3.017294
## Comp.7 Comp.8 Comp.9
## 1 0.07645591 0.07477900 0.08113574
## 2 0.02300838 0.14102601 -0.19460154
## 3 -0.03341952 -0.03913375 -0.79448010
## 4 -0.22054131 0.04841555 -0.76882545
## 5 0.06718604 -0.04797579 -0.32223302
## 6 -0.11178882 -0.14869290 0.69102193Observe que dispone de un número de componentes igual al número de variables, esto es, 9. Estos dos conjuntos de variables presentan las siguientes similitudes y diferencias:
- El nuevo conjunto de variables están incorreladas entre sí. En el caso de que las originales también lo estuvieran coincidirían variables y componentes.
par(mfrow=c(1,2))
corrplot::corrplot(cor(datos), method = "number", type = "lower", number.cex = 0.5)
corrplot::corrplot(cor(componentes$scores), method = "number", type = "lower", number.cex = 0.5)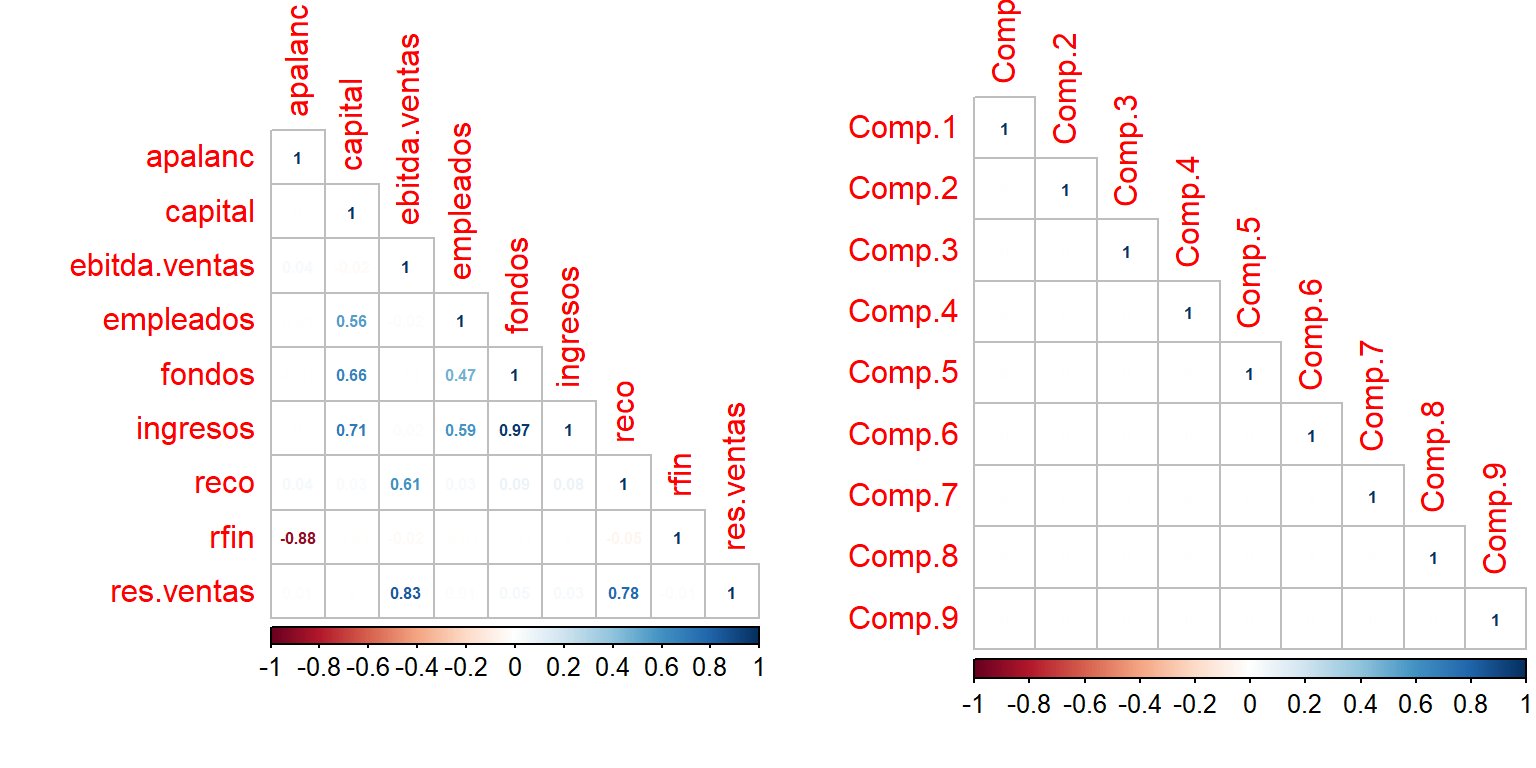
- La suma de las varianzas de todos los componentes principales es igual a la suma de las varianzas de las variables originales. Si los datos están estandarizados, que es equivalente a trabajar en la función
princompcon el argumentocor = TRUE, la suma de varianzas coincide con el número total de variables (9, en este caso). Los componentes principales se proporcionan ordenados en función de la varianza que explican y, habitualmente, basta con un pequeño número de ellos, los primeros, para explicar un elevado porcentaje de la varianza total. Esto permite una reducción de la dimensión al trabajar con un subconjunto de componentes en lugar de con todas las variables originales, con una pequeña pérdida de información.
Paso 3. Determinación del número de componentes a retener
Generalmente, hay un número pequeño de componentes, los primeros, que contienen casi toda la información y el resto suele contribuir relativamente poco. El criterio más sencillo es quedarnos con los componentes que recogen un porcentaje de varianza total que nos parezca suficiente. Existen también otros criterios que nos pueden ayudar a tomar esta decisión. Entre ellos, se encuentra el criterio del autovalor superior a la unidad (regla de Kaiser) y el gráfico de sedimentación (scree test).
Criterio del autovalor superior a la unidad (Regla de Kaiser)
Este criterio retiene aquellos componentes cuyos valores propios son superiores a la unidad y funciona bastante bien salvo con un gran número de variables (más de 40) siendo especialmente preciso con un número pequeño (entre 10 y 15). Las raices de los autovalores asociados a la matriz de correlaciones son las desviaciones típicas de los componentes y se encuentran en $sdev del objeto componentes creado con la función princomp.
autovalores <- componentes$sdev^2
autovalores## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## 3.01981357 2.48024591 1.87560196 0.60329604 0.40053809 0.36376923
## Comp.7 Comp.8 Comp.9
## 0.12100680 0.11563428 0.02009411El número de componentes a retener según este criterio sería 3, ya que únicamente hay 3 autovalores mayores que uno. Como ya se ha visto, esta decisión implicaría quedarnos con un 81.95% de la varianza total de los datos.
Gráfico de sedimentación (scree test)
Este gráfico muestra en el eje de ordenadas los autovalores y en el eje de abscisas los componentes. Los cambios en la pendiente nos permiten observar cuánta capacidad explicativa va aportando cada componente. Se escoge el número de componentes a partir del cual los autovalores restantes son relativamente más pequeños en comparación con él.
plot(componentes, type="lines", main = "Gráfico de sedimentación")
abline(h=1, lty=3, col="red")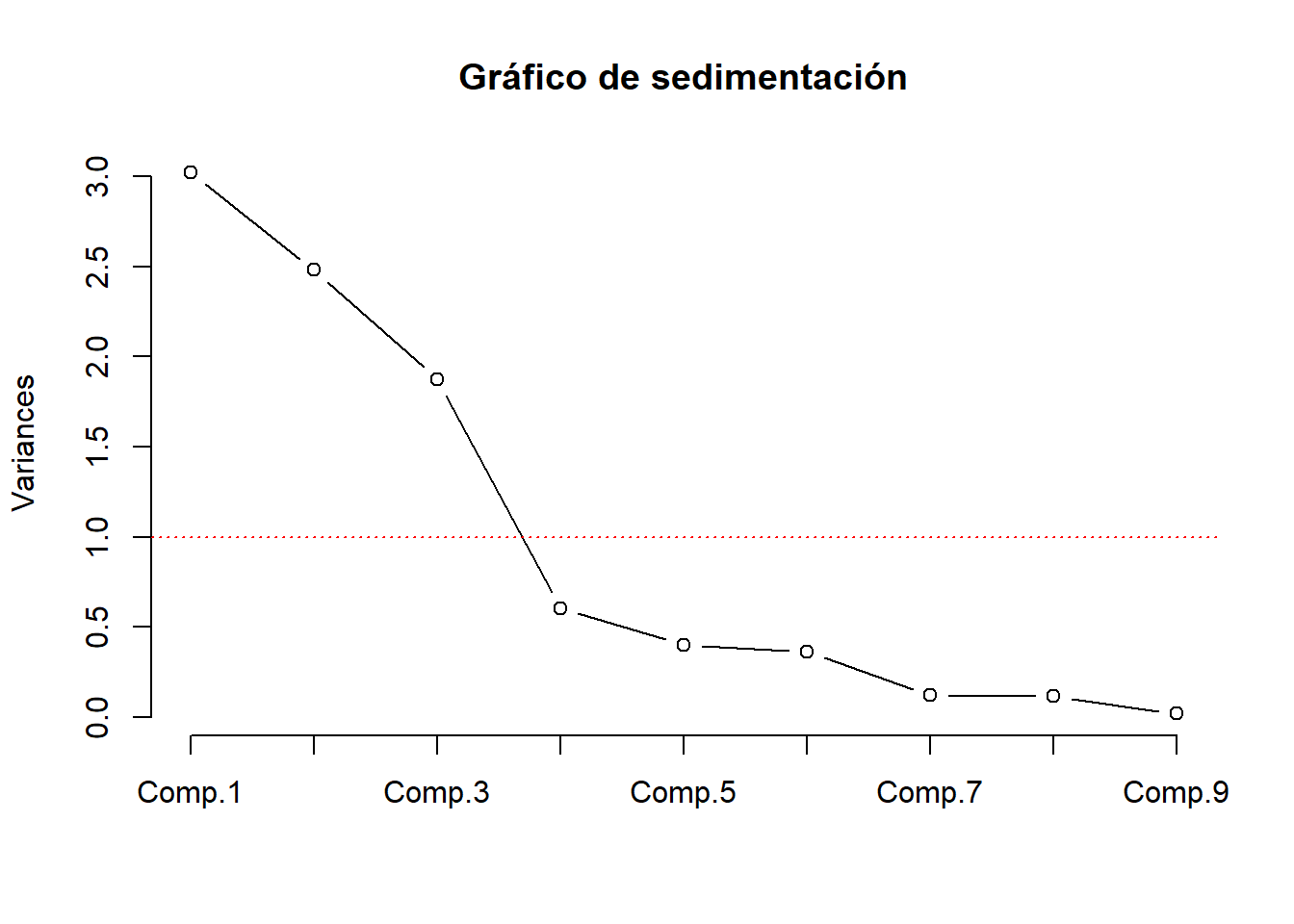
El gráfico de codo nos aconseja también quedarnos con 3 componentes. Ambos criterios ofrecen la misma conclusión, que el número de componentes a retener es 3.
No hay ningún criterio universalmente aceptado, no obstante, el criterio más utilizado es el de los autovalores superiores a la unidad, siempre y cuando se consiga retener con estos componentes un porcentaje de varianza que se considere adecuado para sus propósitos.
Paso 4. Interpretación de los componentes
Para interpretar los componentes debe estudiarse su relación con cada una de las variables originales. Para ello se obtienen e interpretan las correlaciones entre los componentes (componentes$scores) y las variables (datos). Una forma de calcularla es con la función cor:
Cor_CompVar <- round(cor(datos, componentes$scores), 4) # con round se redondea, en este caso concreto, a 4 decimales
Cor_CompVar## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
## apalanc 0.0114 0.1335 0.9610 0.0035 0.0203 0.0180 0.0824
## capital 0.8326 -0.1454 0.0067 0.0630 0.2770 -0.4526 0.0015
## ebitda.ventas 0.1079 0.8858 -0.0922 0.0411 0.3591 0.1840 0.1608
## empleados 0.7217 -0.1202 0.0129 0.6523 -0.1209 0.1549 0.0028
## fondos 0.9099 -0.1004 -0.0044 -0.3531 -0.0447 0.1625 0.0030
## ingresos 0.9490 -0.1259 0.0014 -0.2136 -0.0713 0.1467 -0.0041
## reco 0.1965 0.8474 -0.0654 -0.0353 -0.4131 -0.2287 0.1180
## rfin -0.0201 -0.1302 -0.9614 0.0098 0.0086 0.0119 0.0915
## res.ventas 0.1623 0.9388 -0.1216 0.0208 0.0454 0.0187 -0.2569
## Comp.8 Comp.9
## apalanc 0.2258 0.0053
## capital 0.0038 0.0029
## ebitda.ventas -0.0699 -0.0058
## empleados -0.0073 0.0163
## fondos -0.0133 0.0936
## ingresos 0.0155 -0.1047
## reco -0.0312 0.0008
## rfin 0.2227 0.0050
## res.ventas 0.0932 0.0032También se puede recurrir a la función get_pca_var del paquete factoextra:
factoextra::get_pca_var(componentes)## Principal Component Analysis Results for variables
## ===================================================
## Name Description
## 1 "$coord" "Coordinates for the variables"
## 2 "$cor" "Correlations between variables and dimensions"
## 3 "$cos2" "Cos2 for the variables"
## 4 "$contrib" "contributions of the variables"Esta función proporciona en su salida las coordenadas de las variables en los componentes ($coord), las correlaciones entre las variables y los componentes ($cor), la calidad de la representación de las variables en los componentes ($cos2) y el peso de las variables en la definición de los componentes ($contrib).
round(factoextra::get_pca_var(componentes)$cor, 4) # con round se redondea, en este caso concreto, a 4 decimales## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7
## apalanc 0.0114 0.1335 0.9610 0.0035 0.0203 0.0180 0.0824
## capital 0.8326 -0.1454 0.0067 0.0630 0.2770 -0.4526 0.0015
## ebitda.ventas 0.1079 0.8858 -0.0922 0.0411 0.3591 0.1840 0.1608
## empleados 0.7217 -0.1202 0.0129 0.6523 -0.1209 0.1549 0.0028
## fondos 0.9099 -0.1004 -0.0044 -0.3531 -0.0447 0.1625 0.0030
## ingresos 0.9490 -0.1259 0.0014 -0.2136 -0.0713 0.1467 -0.0041
## reco 0.1965 0.8474 -0.0654 -0.0353 -0.4131 -0.2287 0.1180
## rfin -0.0201 -0.1302 -0.9614 0.0098 0.0086 0.0119 0.0915
## res.ventas 0.1623 0.9388 -0.1216 0.0208 0.0454 0.0187 -0.2569
## Dim.8 Dim.9
## apalanc 0.2258 0.0053
## capital 0.0038 0.0029
## ebitda.ventas -0.0699 -0.0058
## empleados -0.0073 0.0163
## fondos -0.0133 0.0936
## ingresos 0.0155 -0.1047
## reco -0.0312 0.0008
## rfin 0.2227 0.0050
## res.ventas 0.0932 0.0032Estos coeficientes que se acaban de calcular son los que se utilizan para interpretar los componentes. Como se ha decidido retener solo tres componentes, es conveniente crear un objeto que contenga solo las correlaciones con esos tres componentes, que será el objeto a analizar:
Cor_CompVar_retenidos <- Cor_CompVar[, 1:3]
Cor_CompVar_retenidos## Comp.1 Comp.2 Comp.3
## apalanc 0.0114 0.1335 0.9610
## capital 0.8326 -0.1454 0.0067
## ebitda.ventas 0.1079 0.8858 -0.0922
## empleados 0.7217 -0.1202 0.0129
## fondos 0.9099 -0.1004 -0.0044
## ingresos 0.9490 -0.1259 0.0014
## reco 0.1965 0.8474 -0.0654
## rfin -0.0201 -0.1302 -0.9614
## res.ventas 0.1623 0.9388 -0.1216Calidad de la representación
Antes de proceder a la interpretación de los componentes, es conveniente analizar si con el número de componentes elegido (tres) están todas las variables bien representadas. Para ello se utiliza el coeficiente de correlación al cuadrado:
round(Cor_CompVar[,1:3]^2, 4) # con round se redondea, en este caso concreto, a 4 decimales## Comp.1 Comp.2 Comp.3
## apalanc 0.0001 0.0178 0.9235
## capital 0.6932 0.0211 0.0000
## ebitda.ventas 0.0116 0.7846 0.0085
## empleados 0.5209 0.0144 0.0002
## fondos 0.8279 0.0101 0.0000
## ingresos 0.9006 0.0159 0.0000
## reco 0.0386 0.7181 0.0043
## rfin 0.0004 0.0170 0.9243
## res.ventas 0.0263 0.8813 0.0148o con $cos2 en la función get_pca_var:
round(factoextra::get_pca_var(componentes)$cos2[, 1:3], 4) # con round se redondea, en este caso concreto, a 4 decimales## Dim.1 Dim.2 Dim.3
## apalanc 0.0001 0.0178 0.9235
## capital 0.6932 0.0211 0.0000
## ebitda.ventas 0.0116 0.7846 0.0085
## empleados 0.5209 0.0144 0.0002
## fondos 0.8279 0.0101 0.0000
## ingresos 0.9007 0.0158 0.0000
## reco 0.0386 0.7180 0.0043
## rfin 0.0004 0.0170 0.9243
## res.ventas 0.0263 0.8813 0.0148Estos resultados se pueden visualizar con corrplot:
corrplot::corrplot(factoextra::get_pca_var(componentes)$cos2[, 1:3], is.corr = F)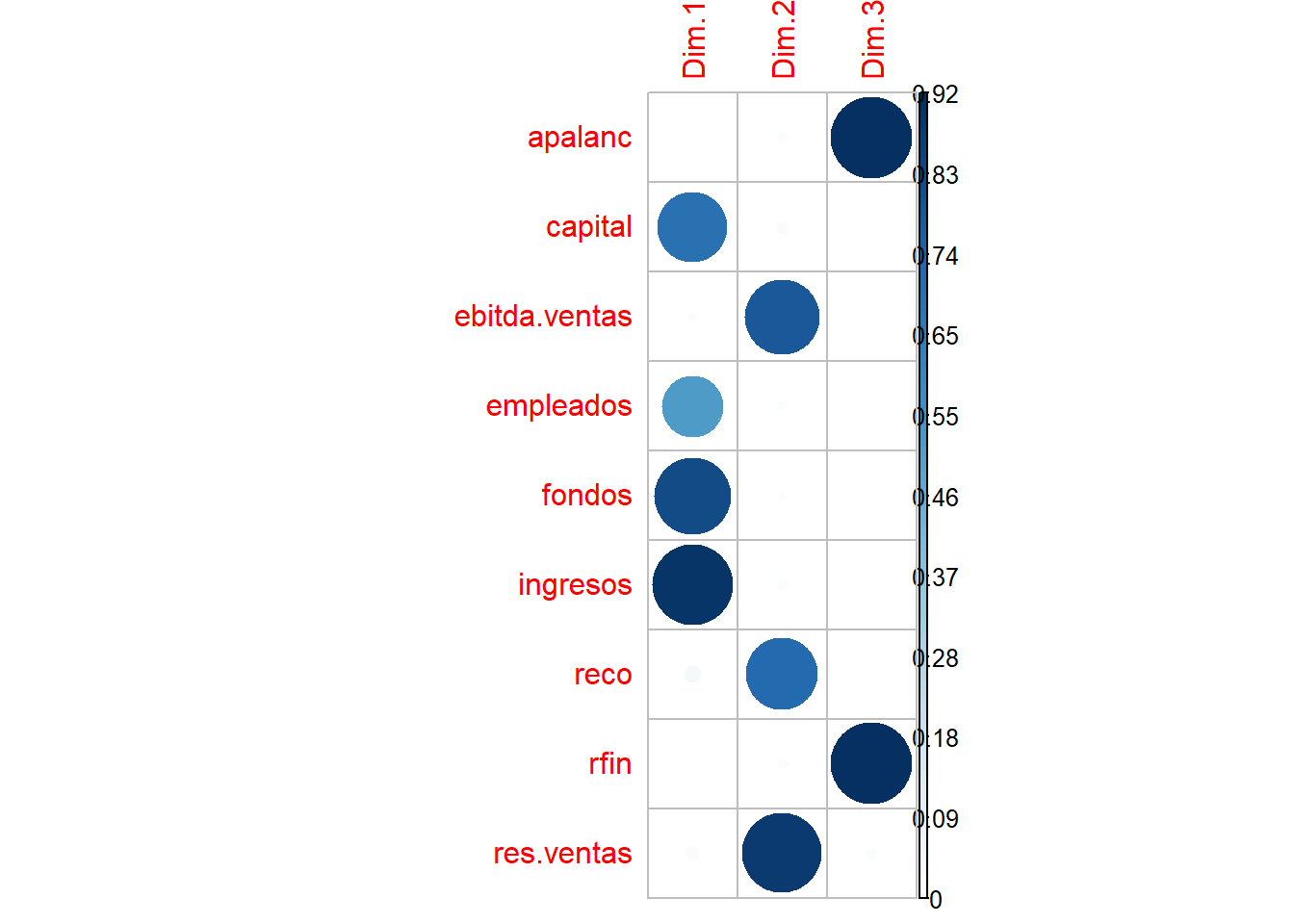
El valor de la correlación al cuadrado (cos2) se utiliza para estimar la calidad de la representación. Cuanto más cercano esté a la unidad, mejor será esta. La variable apalanc, por ejemplo, está explicada fundamentalmente por la dimensión 3 (componente 3), lo mismo que le ocurre a la variable rfin. Ambas presentan un color azul intenso, lo que indica un porcentaje de varianza explicada cercano al 92%.
Si consideráramos dos componentes (por ejemplo, los componentes 1 y 2) se puede emplear otro gráfico, con la función fviz_pca_var del paquete factoextra, donde sobre un círculo de radio unidad, se sitúan las variables, utilizando como coordenadas sus correlaciones con cada uno de los componentes en el plano. Además, las variables se pueden colorear en función de distintas características, entre las que destacan su contribución y el valor del cos2 (por ejemplo, verde, naranja o rojo dependiendo de que sean valores bajos, medios o altos, respectivamente). Si optamos por colorear en función del valor del cos2 tenga en cuenta que, el representado en el gráfico para una variable, por ejemplo, rfin, es la suma de los cos2 de los dos primeros componentes en la matriz anterior:
\[0.0004+ 0.0170=0.0174\] Esto indica que el plano formado por dichos componentes solo explica el 1.74% de la varianza de rfin, lo que significa que está pobremente representado por estas dos dimensiones.
factoextra::fviz_pca_var(componentes, col.var = "cos2",
gradient.cols = c("green", "orange", "red"),
repel = TRUE,
title = "Cos2 de las variables en el plano 1-2")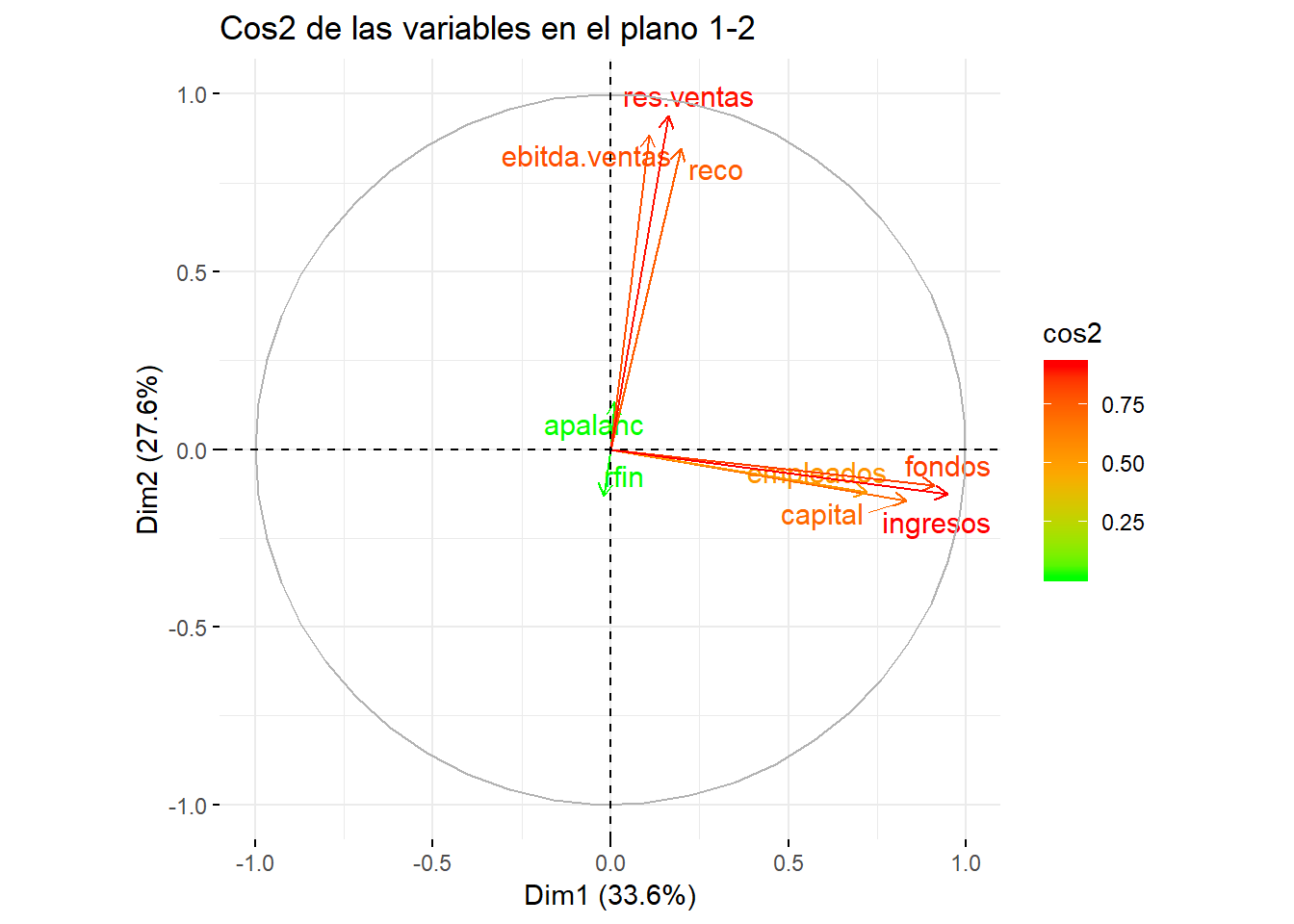
Cuanto más cercana esté una variable al borde del círculo, mejor será la calidad de la representación en el conjunto de los dos componentes. Las variables que están cercanas al centro del círculo no están suficientemente bien representadas por esos componentes. En este caso, todas las variables están bien representadas por estas dos dimensiones, excepto las variables apalanc y rfin que, como se comentó anteriormente están explicadas fundamentalmente por el componente 3. Observe que, tanto res.ventas como ingresos están muy bien representadas en el plano, dado que están cerca del círculo unidad y están coloreadas en rojo. Sin embargo, la variable res.ventas está fundamentalmente explicada por el componente 2, de ahí su cercanía a este eje (Dim2) y la variable ingresos por el componente 1, de ahí la proximidad a ese eje (Dim1).
Un último gráfico que puede emplear es el proporcionado por el paquete factoextra. Puede utilizarse para representar el valor del cos2 para uno o varios componentes. En el caso de querer recoger simultáneamente la información para los tres componentes, el gráfico sería:
factoextra::fviz_cos2(componentes, choice = "var",
axes = 1:3, # axes recoge los componentes a utilizar
title = "Cos2 de las variables para los componentes 1 a 3") 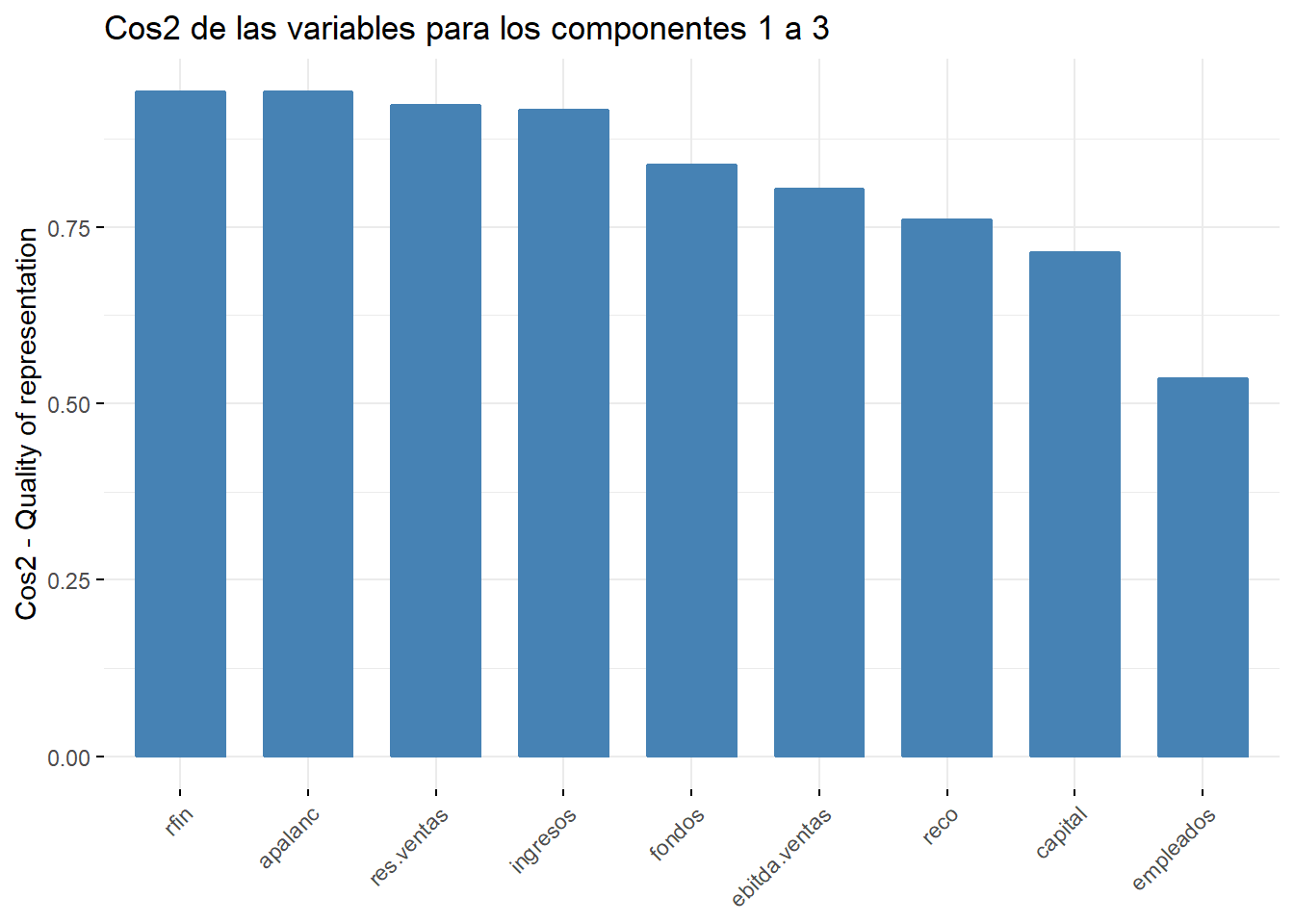
En este caso, se representa la suma de cos2 para los tres componentes. Por ejemplo, para la variable rfin
\[0.0004+ 0.0170+ 0.9243=0.9417\]
Al considerar tres componentes la variable rfin está bien representada. De hecho, la proporción de variabilidad explicada por los tres componentes retenidos es superior al 80% en la mayoría de las variables, siendo la más baja la de la variable empleados. Esto indica que, en general, las variables están bien representadas por los tres componentes.
Si quiere conocer la calidad de la representación de cada variable con los tres componentes puede emplear:
apply(factoextra::get_pca_var(componentes)$cos2[, 1:3], 1, sum)## apalanc capital ebitda.ventas empleados fondos
## 0.9414426 0.7144092 0.8047719 0.5355003 0.8379590
## ingresos reco rfin res.ventas
## 0.9165423 0.7609235 0.9416785 0.9224342Cálculo de las contribuciones
Para determinar la importancia que tiene cada variable en un componente concreto se calculan las contribuciones. Se define como el porcentaje de varianza del componente explicado por la variable. Así, por ejemplo, teniendo en cuenta que la varianza del componente 1 es 3.01981357, la contribución de la variable capital en dicho componente es:
\[\frac{0.8326^2}{3.01981357}=0.2296\] Este valor indica que la variable capital explica el 22.96% de la variabilidad del componente 1. La información acerca de las contribuciones, en porcentaje, se encuentra en el elemento :
round(factoextra::get_pca_var(componentes)$contrib[, 1:3], 4) # Se redondea a cuatro decimales## Dim.1 Dim.2 Dim.3
## apalanc 0.0043 0.7183 49.2373
## capital 22.9559 0.8523 0.0024
## ebitda.ventas 0.3853 31.6354 0.4533
## empleados 17.2494 0.5820 0.0088
## fondos 27.4144 0.4063 0.0010
## ingresos 29.8262 0.6389 0.0001
## reco 1.2792 28.9496 0.2278
## rfin 0.0134 0.6839 49.2808
## res.ventas 0.8720 35.5333 0.7885Estos valores pueden ayudar a la interpretación de los componentes. A modo de ejemplo, las variables apalanc y rfin explican cada una de ellas en torno al 50% de la variabilidad del componente 3.
Descripción de los componentes
Para describir cada componente hay que identificar las variables cuyas correlaciones con el componente son más elevadas en valor absoluto. Cuando es positiva (negativa) la relación entre el componente y dicha variable es directa (inversa). Además, debe ser posible determinar el significado de un componente a partir de las variables con las que tiene una relación fuerte y poner nombre a los componentes de acuerdo con la estructura de las correlaciones.
Para llevar a cabo esta interpretación puede resultar útil visualizar exclusivamente las correlaciones más altas en valor absoluto de forma que la atención se centre en ellas.
Cor_CompVar_retenidos_mayores <- Cor_CompVar_retenidos
Cor_CompVar_retenidos_mayores[abs(Cor_CompVar_retenidos_mayores) < 0.4]<- NA
print(Cor_CompVar_retenidos_mayores, na.print="")## Comp.1 Comp.2 Comp.3
## apalanc 0.9610
## capital 0.8326
## ebitda.ventas 0.8858
## empleados 0.7217
## fondos 0.9099
## ingresos 0.9490
## reco 0.8474
## rfin -0.9614
## res.ventas 0.9388Teniendo en cuenta esta información, puede interpretarse que:
Componente 1: Las variables
capital,empleados,fondoseingresospresentan correlaciones con el componente 1 superiores a 0.7, indicando que están muy correlacionados con él. Esto es, cuanto mayor sea el valor de estas cuatro variables en una empresa, mayor será su puntuación en este componente. Dada la naturaleza de estas variables, este componente representa el tamaño de la empresa.Componente 2: Las variables
ebitda.ventas,recoyres.ventaspresentan correlaciones superiores a 0.85 con el componente 2. Esta componente podría representar, por tanto, la rentabilidad de la empresa. Cuanto más rentable sea la empresa, mayor puntuación tendrá esta en el segundo componente.Componente 3: Finalmente las variables
apalancyrfindefinen el componente 3, que está relacionado, de esta forma, con el endeudamiento de la empresa. Cuanto mayor sea el apalancamiento de una empresa y menor sea la rentabilidad financiera, mayor puntuación alcanzará en el componente, lo que indicará, normalmente, un mayor endeudamiento de la empresa.
También se pueden realizar representaciones gráficas que nos ayuden a interpretar los componentes dos a dos. Por ejemplo, para el primer y segundo componente:
plot(Cor_CompVar_retenidos[, 1], Cor_CompVar_retenidos[, 2], pch = 20,
xlab = "Dim1", ylab = "Dim2",
main = "Variables en el plano 1-2") # punto negro en los gráficos
text(Cor_CompVar_retenidos[, 1], Cor_CompVar_retenidos[, 2],
labels = row.names(Cor_CompVar_retenidos), # Etiquetas de las variables
cex= 0.8, # Tamaño de letra
pos = 4) # Posición de la etiqueta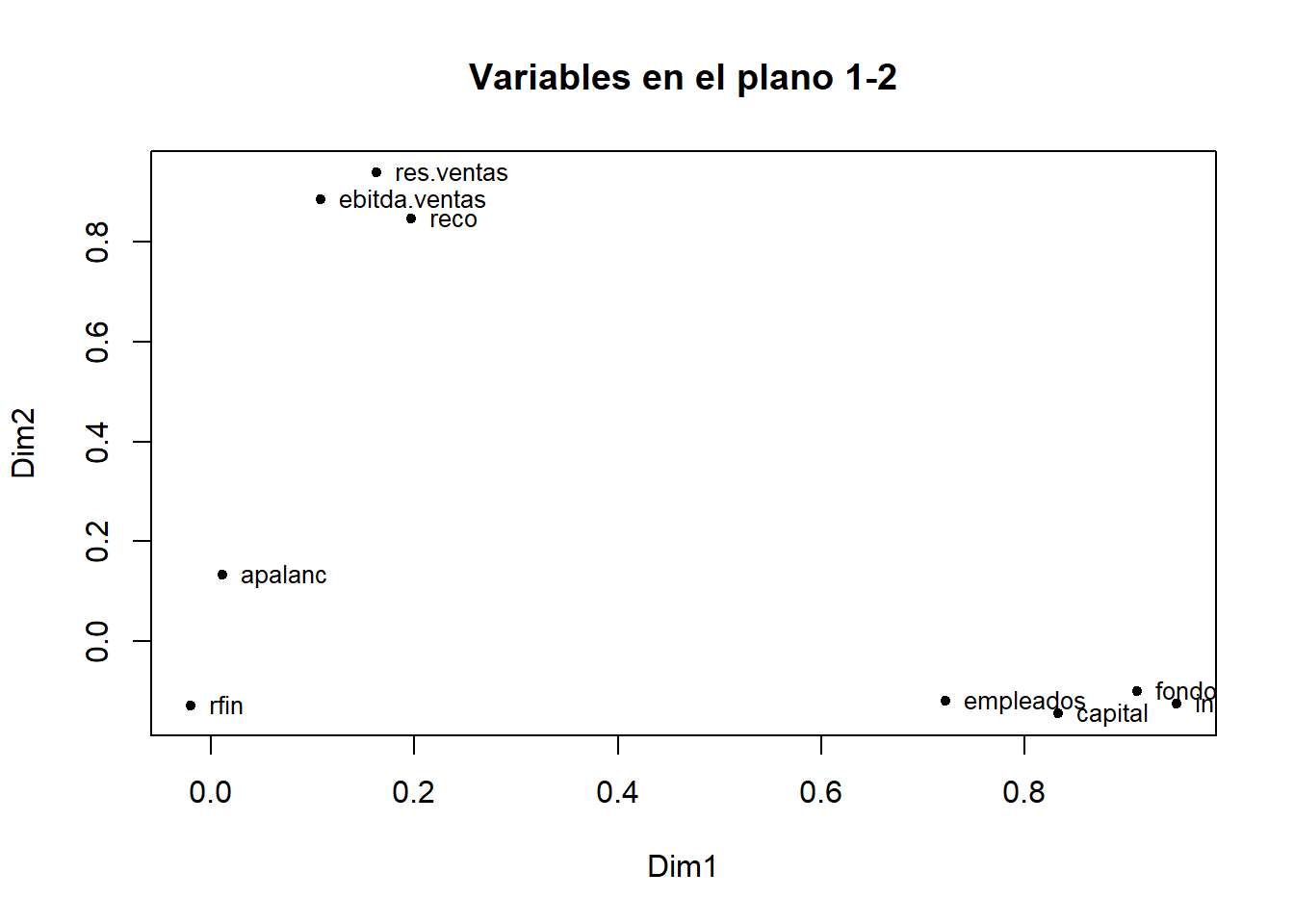
En este gráfico se puede ver como capital, empleados, fondos e ingresos presentan correlaciones altas en el componente 1 (alrededor de 0.8) y bajas en el componente 2, es decir, están próximos al eje X y alejados del origen de coordenadas, indicando que estas variables definen al componente 1. Por otro lado, el componente 2 está representado por las variables ebitda.ventas, reco y res.ventas, ya que se sitúan próximas al eje Y y alejadas del origen de coordenadas (correlación alrededor de 0.8). Por último, las variables apalanc y rfin al estar cercanas al origen tienen correlaciones muy bajas con los dos primeros componentes, por lo que no definen a ninguno de los componentes representados en este gráfico.
También se puede recurrir a los gráficos disponibles en el paquete factoextra, como los proporcionados por la función fviz_pca_var, que resultan mucho más atractivos:
factoextra::fviz_pca_var(componentes,
col.var = "contrib", # Indica por colores el valor de las contribuciones
gradient.cols = c("green", "orange", "red"),
repel = TRUE, # Evita que se solapen los nombres de las variables
title = "Contribución de las variables en el plano 1-2") 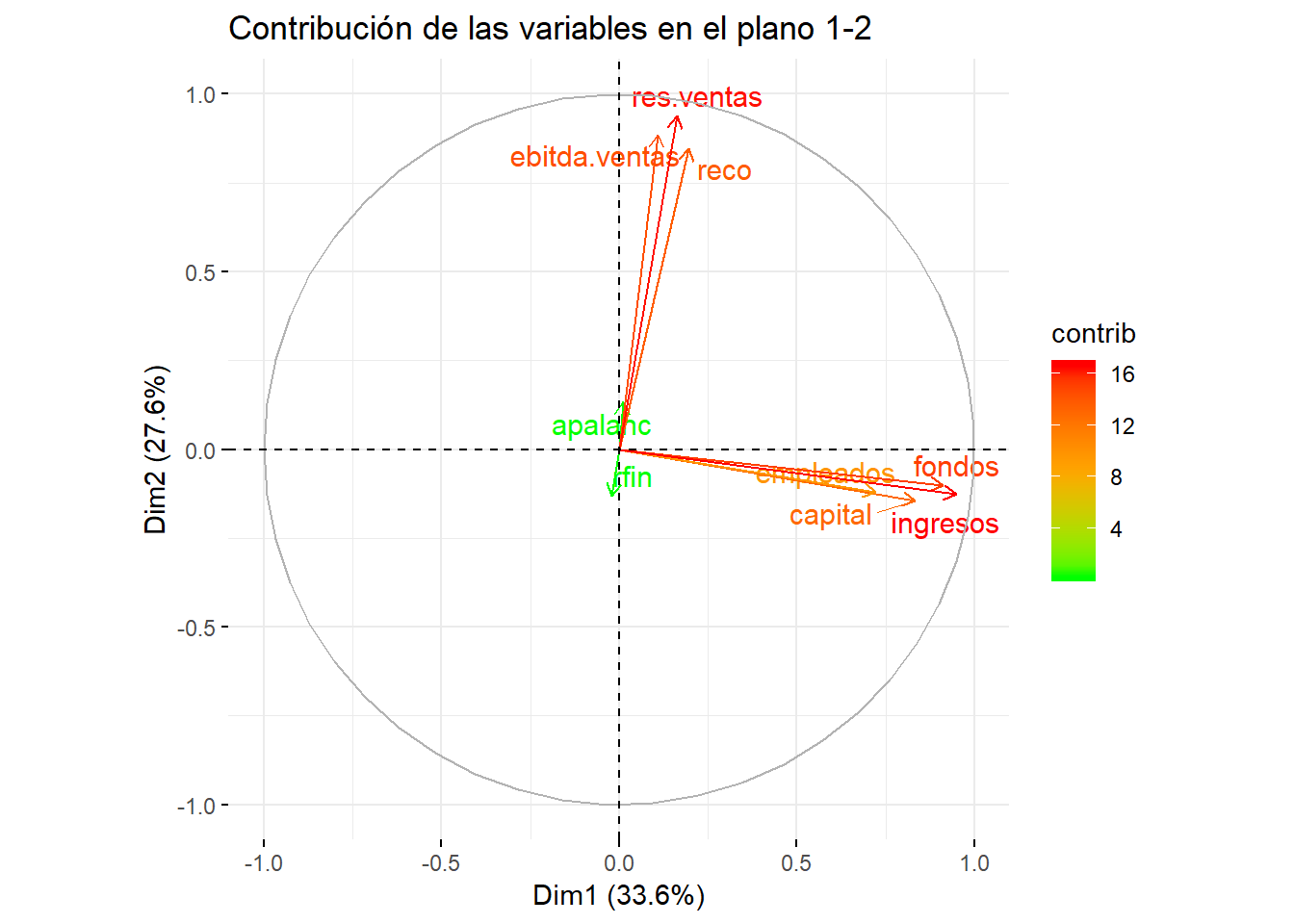
La interpretación de este gráfico es similar a la del anterior, pero con elementos adicionales como son la representación de una circunferencia de radio uno y el uso de colores. Recuerde que en este gráfico cuanto mayor es la correlación entre una variable y un componente, más próxima está esta variable a la circunferencia y al eje representado por ese componente, indicando que es importante en la definición del mismo. En este caso, con el color se representan las contribuciones (verde, naranja o rojo dependiendo que sean valores bajos, medios o altos, respectivamente). Observe que apalanc y rfin aparecen de color verde lo que indica que estas variables no contribuyen a explicar ninguno de estos dos componentes (Dim1 y Dim2).
Se puede realizar estos gráficos el resto de combinaciones de dos componentes:
factoextra::fviz_pca_var(componentes,
axes = c(1,3), # Si se desea una combinación de dimensiones que no sea la de los dos primeros componentes
col.var = "contrib", # Indica por colores el valor de las contribuciones
gradient.cols = c("green", "orange", "red"),
repel = TRUE, # Evita que se solapen los nombres de las variables
title = "Contribución de las variables en el plano 1-3") 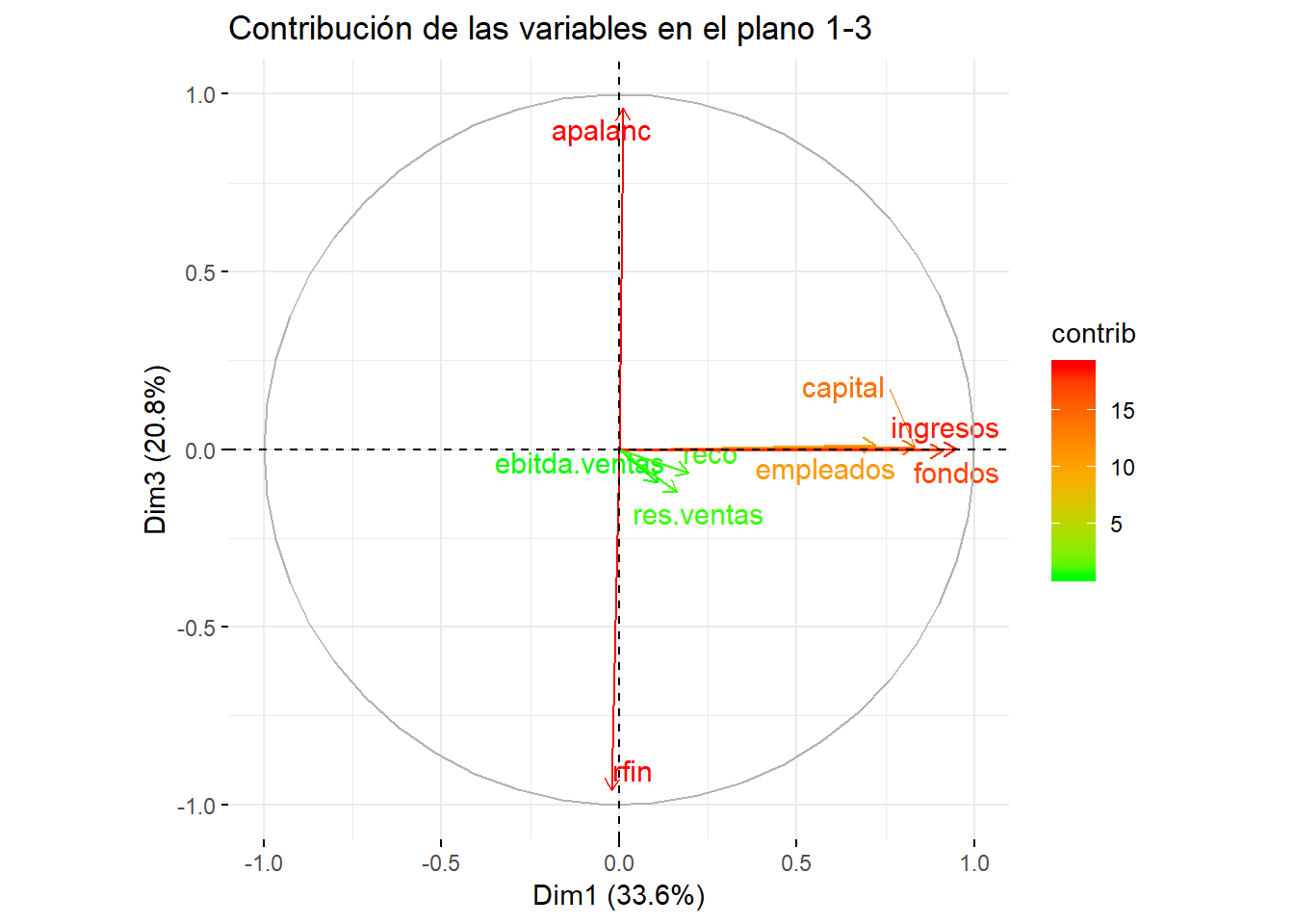
factoextra::fviz_pca_var(componentes,
axes = c(2,3), # Si se desea una combinación de dimensiones que no sea la de los dos primeros componentes
col.var = "contrib", # Indica por colores el valor de las contribuciones
gradient.cols = c("green", "orange", "red"),
repel = TRUE, # Evita que se solapen los nombres de las variables
title = "Contribución de las variables en el plano 2-3") 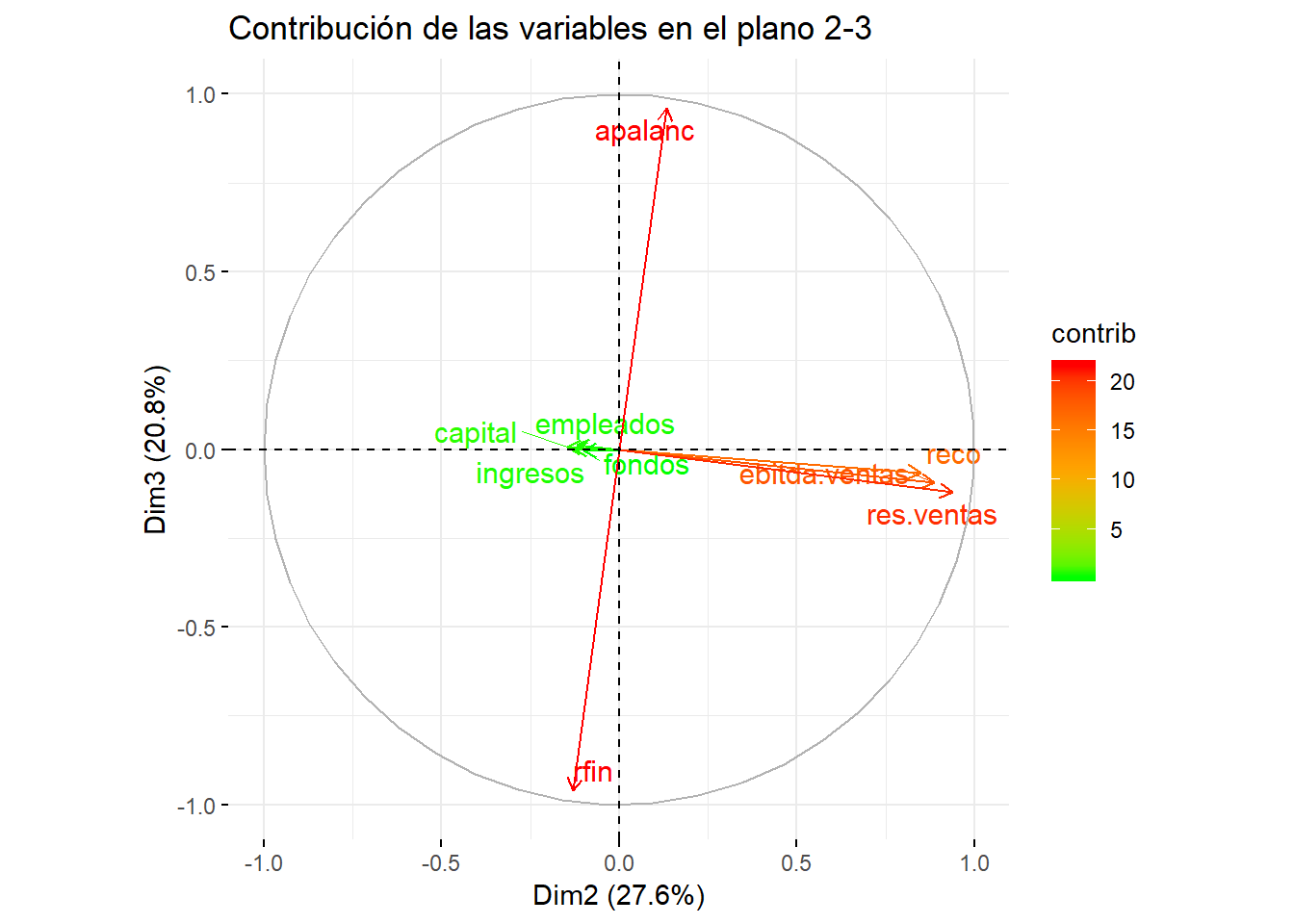
En estos dos últimos gráficos apalanc y rfin aparecen cercanas a la circunferencia y al componente 3, pero con signos diferentes, y de color rojo, mostrando que son estas variables las que definen a dicho componente.
La matriz de puntuaciones de cada empresa en el nuevo espacio formado por los tres componentes retenidos puede obtenerse a través del objeto $scores:
matriz_nueva <- componentes$scores[ , 1:3]O utilizando la función get_pca_ind:
matriz_nueva <- factoextra::get_pca_ind(componentes)$coord[, 1:3]Esa información también puede representarse gráficamente, para cualquier combinación de los componentes que desee. Por ejemplo, para los componentes 1 y 2 se obtiene el siguiente gráfico:
factoextra::fviz_pca_ind(componentes, axes = c(1, 2),
title = "Empresas en el plano 1-2") 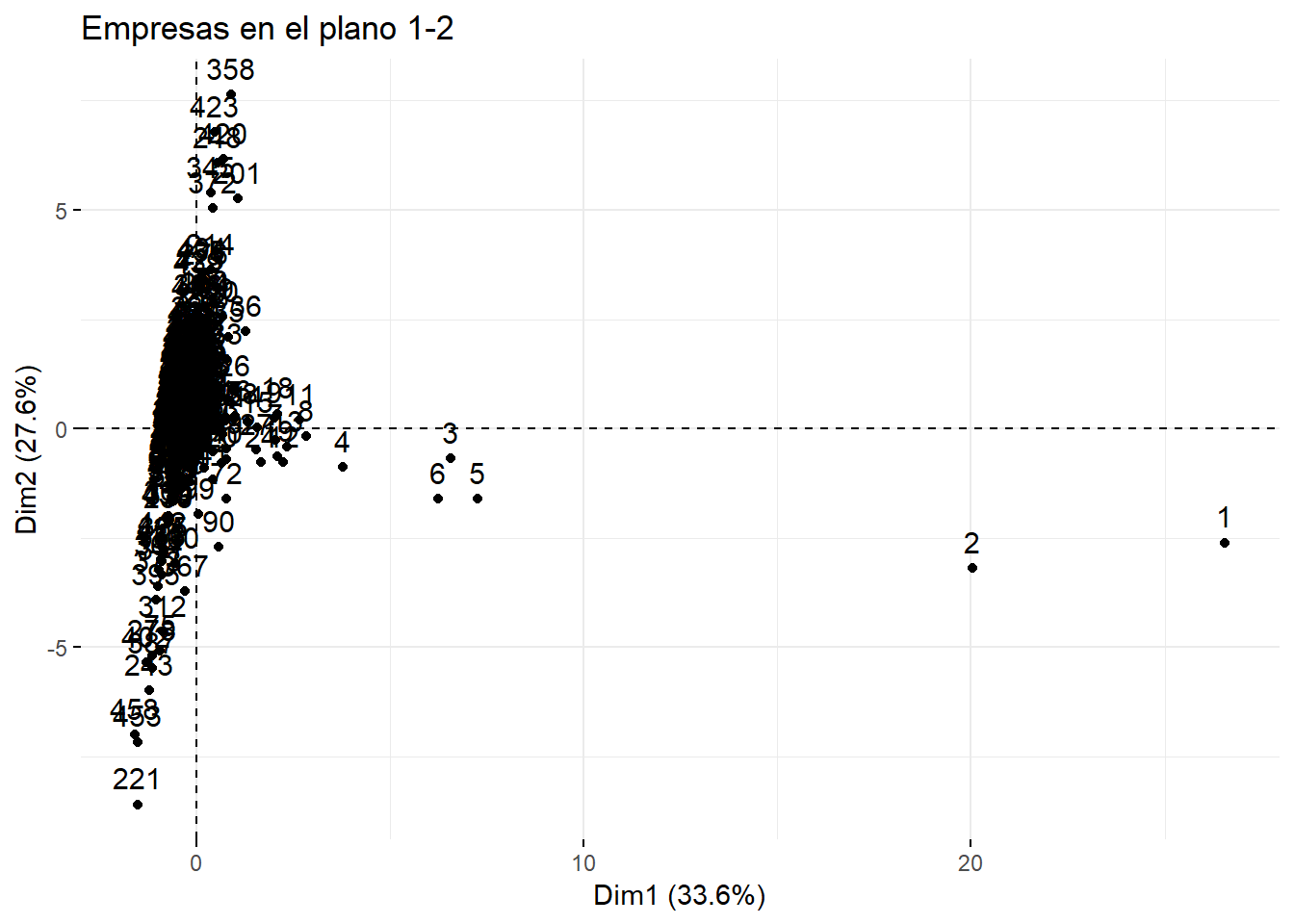
donde se puede ver que las empresas 1 a 6 son las de mayor tamaño, porque son las que toman valores mayores en la dimensión 1. Observe, no obstante, que esta conclusión solo debería aplicarse a las empresas que verdaderamente estén bien representadas en este plano. Por ejemplo, si de todas las empresas seleccionamos la mitad que están mejor representadas en este plano (aproximadamente 225 empresas) esta información se puede incorporar al gráfico anterior en el argumento select.ind:
factoextra::fviz_pca_ind(componentes, axes = c(1, 2),
select.ind = list(cos2=225), # 225 empresas mejor representadas por este plano (mayor valor de cos2)
title = "Empresas con mayor cos2 en el plano 1-2") 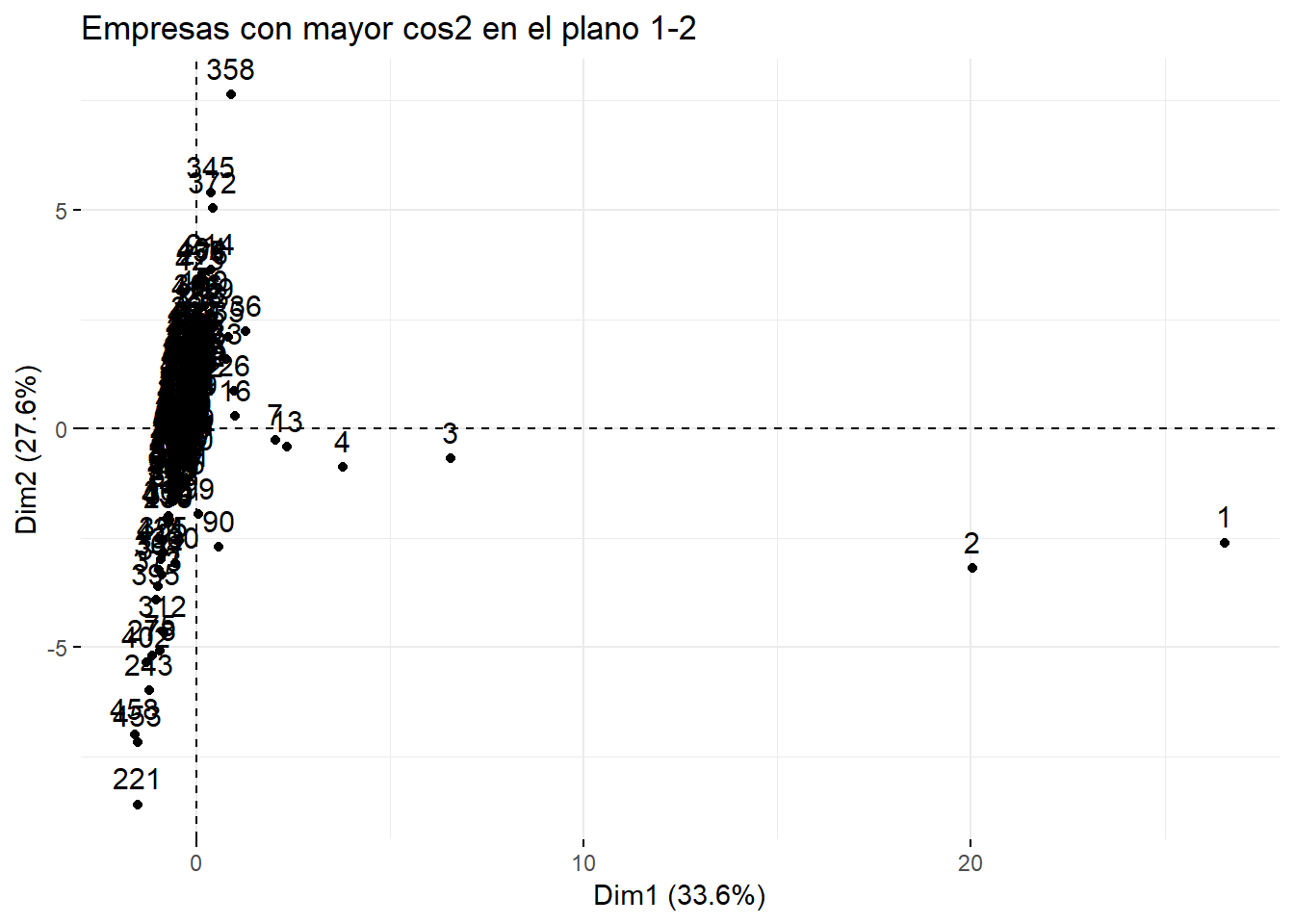
Si tiene interés en ver cuál es el valor mínimo del cos2 de las empresas que está representando puede emplear:
cos2_12 <- apply(factoextra::get_pca_ind(componentes)$cos2[,1:2], 1, sum) # calcula cos2 para las dimensiones del plano
cos2_12_ord <- order(cos2_12, decreasing = T) # ordena el cos2 de menor a mayor
cos2_12[cos2_12_ord[225]] # ofrece el valor de cos2 que ocupa la posición señalada## 237
## 0.6973814Del gráfico anterior puede deducir que las empresas 1 a 4 están bien representadas en este plano, y se caracterizan principalmente por su gran tamaño. Se advierte, además, la diferencia entre algunas empresas en función de su rentabilidad. Por ejemplo, la empresa 221 se caracteriza por una baja rentabilidad, frente a la 358 cuya rentabilidad es alta.
Además de representar gráficamente la información, también puede emplearla como punto de partida para realizar análisis posteriores, como regresión o conglomerados, en los que no utilizará la matriz original de datos, sino la nueva matriz que contiene la puntuación de las empresas en los componentes retenidos.
Rotación de los ejes
En este ejercicio, las variables cargan mucho en un componente (coeficientes de correlación altos en valor absoluto) y muy poco en los demás, por lo que es fácil identificar la estructura de los componentes. Sin embargo, esto no sucede siempre y, en esos casos, es aconsejable realizar una rotación de ejes. Uno de los métodos más usados es la rotación Varimax que minimiza el número de variables que tienen correlaciones altas en valor absoluto en cada componente.
Cor_CompVar_rotadas <- varimax(Cor_CompVar[, 1:3])
Cor_CompVar_rotadas$loadings##
## Loadings:
## Comp.1 Comp.2 Comp.3
## apalanc 0.970
## capital 0.845
## ebitda.ventas 0.896
## empleados 0.732
## fondos 0.914
## ingresos 0.957
## reco 0.870
## rfin -0.970
## res.ventas 0.960
##
## Comp.1 Comp.2 Comp.3
## SS loadings 3.006 2.485 1.884
## Proportion Var 0.334 0.276 0.209
## Cumulative Var 0.334 0.610 0.820Varimax proporciona directamente la matriz de componentes rotados (Cor_CompVar_rotadas$loadings). Antes de proseguir, recuerde que funciones diferentes pueden utilizar el mismo nombre para resultados diferentes. Este es el caso de $loadings que, como resultado de la función varimax, proporciona los coeficientes de correlación, mientras que como resultado de la función princomp proporciona los coeficientes de las combinaciones lineales.
Si desea representar gráficamente el objeto Cor_CompVar_rotadas$loadings, puede utilizar la función plot. Puede también incluir información adicional que haga que el gráfico sea similar a los que se obtienen a través de las funciones del paquete factoextra. Por ejemplo, para los dos primeros componentes:
plot(Cor_CompVar_rotadas$loadings[, 1], Cor_CompVar_rotadas$loadings[, 2],
xlab = "Componente 1", ylab = "Componente 2", # Rótulos de los ejes
xlim = c(-1,1), ylim = c(-1,1), asp = 1, cex = 0.8, # Límites, aspecto y tamaño
pch = 20) # Tipo de símbolo
text(Cor_CompVar_rotadas$loadings[, 1], Cor_CompVar_rotadas$loadings[, 2],
labels = row.names(Cor_CompVar_rotadas$loadings), # Etiquetas de las variables
cex= 0.8) # Tamaño de letra
abline(v = 0, h = 0, lty = 3) # Ejes de coordenadas
symbols(0, 0, circles = 1, add = TRUE, inches = FALSE) # Círculo de radio unidad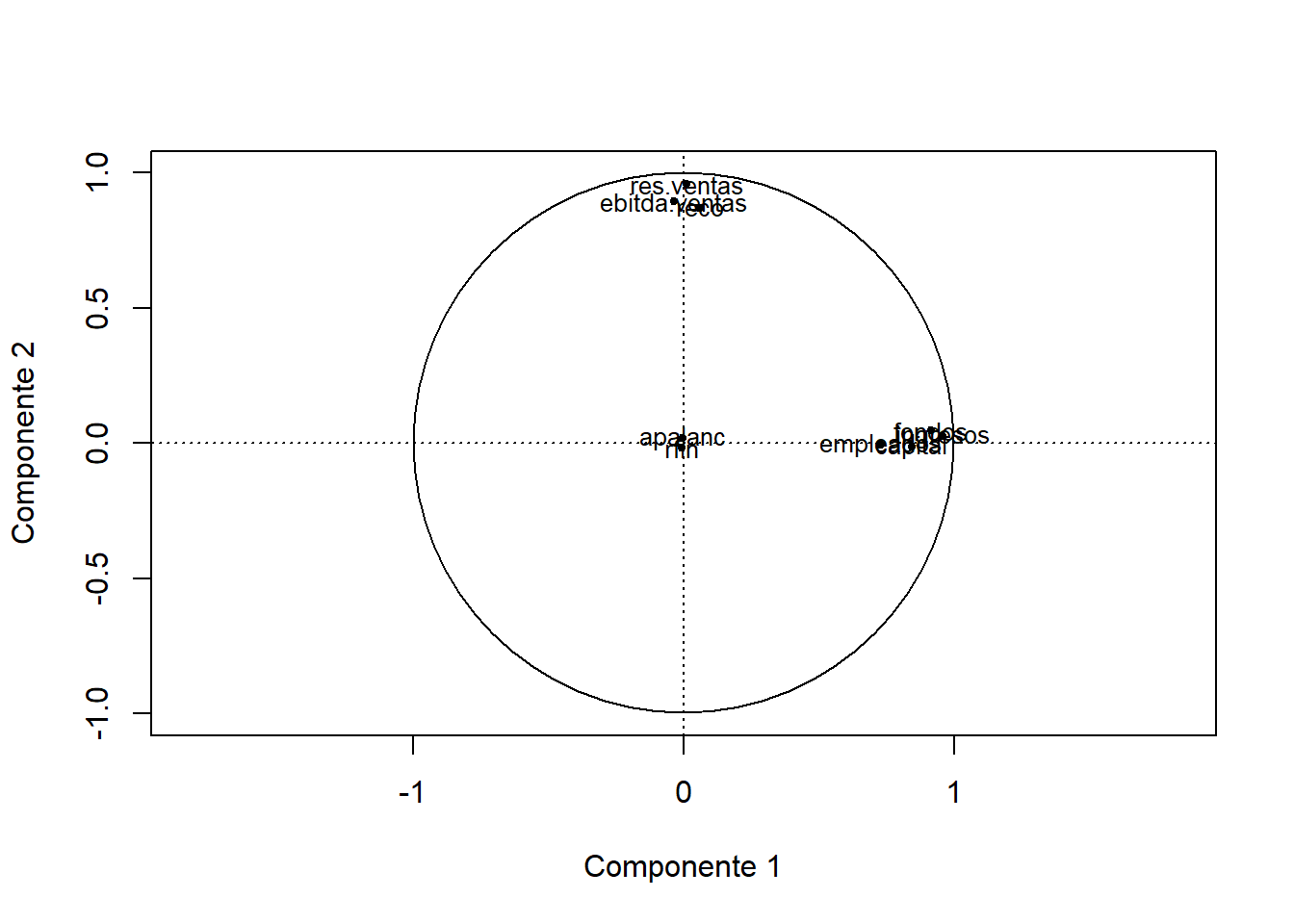
En el caso de haber rotado los componentes, para obtener las puntuaciones en el espacio de los ejes rotados, la matriz de puntuaciones debe multiplicarse por la matriz de rotación, que también está disponible como salida de la función varimax. En nuestro caso concreto, en el que se han retenido tres componentes, el resultado es:
matriz_nueva_rotada <- as.data.frame(componentes$scores[, 1:3] %*% Cor_CompVar_rotadas$rotmat)
names(matriz_nueva_rotada) <- c("Comp.1", "Comp.2", "Comp.3")La representación de las puntuaciones en los dos primeros componentes para el conjunto de empresas:
plot(matriz_nueva_rotada$Comp.1, matriz_nueva_rotada$Comp.2,
xlab = "Componente 1", ylab = "Componente 2", # Títulos de los ejes
pch = 20)
text(matriz_nueva_rotada$Comp.1, matriz_nueva_rotada$Comp.2,
labels = row.names(matriz_nueva_rotada), # Etiquetas de las variables
cex= 0.8, pos = 3) # Tamaño de letra y posición de la etiqueta
abline(v = 0, h = 0, lty = 3)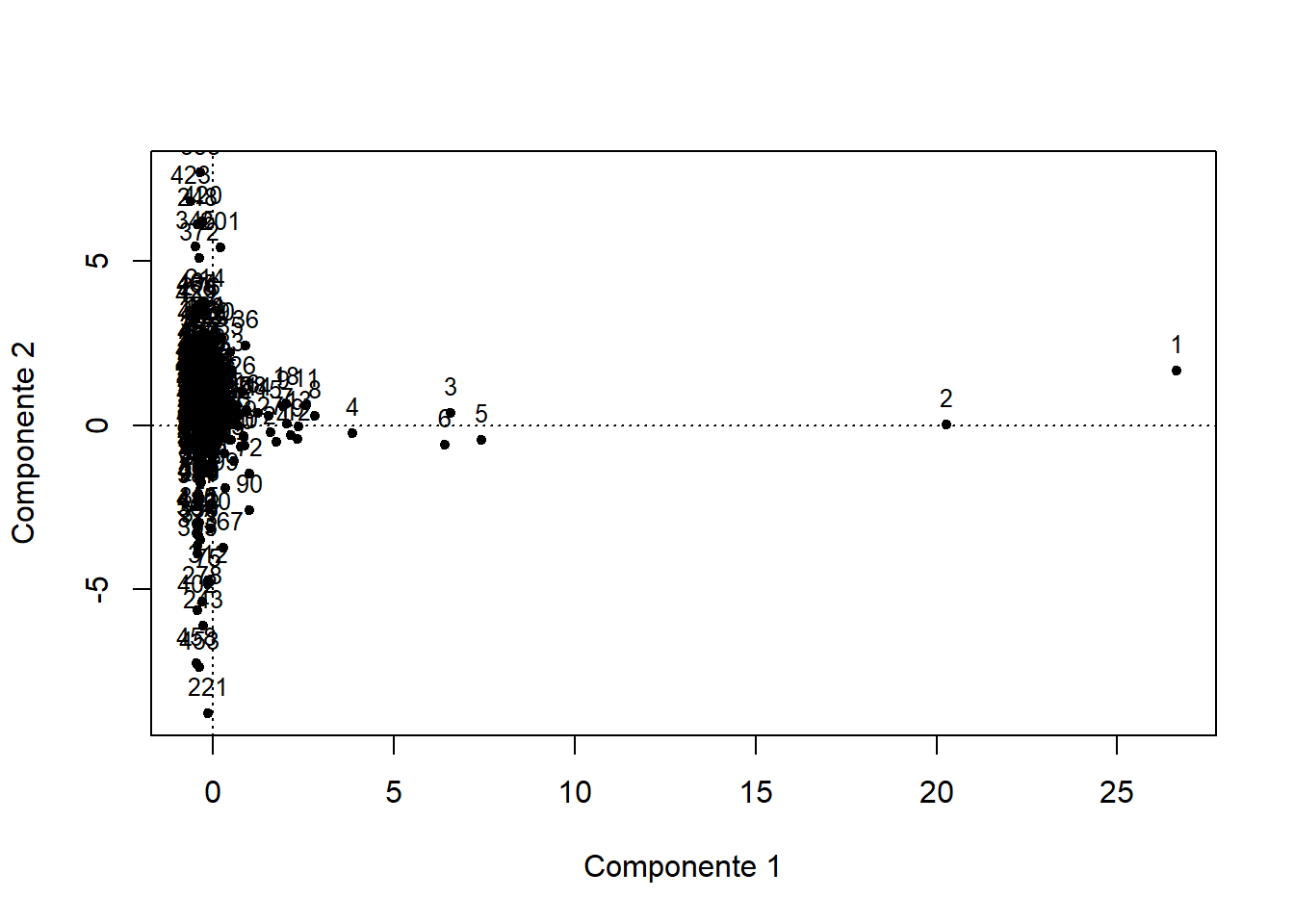
Análisis de componentes principales utilizando FactoMineR
El análisis de componentes principales también se puede llevar a cabo utilizando la función PCA del paquete FactoMineR. La función proporciona como salida los resultados que ya se han analizado en apartados anteriores, y los representa gráficamente. Esta función se encuentra, además, implementada en forma de aplicación shiny en el paquete Factoshiny.
pca <- FactoMineR::PCA(datos, ncp = 3) 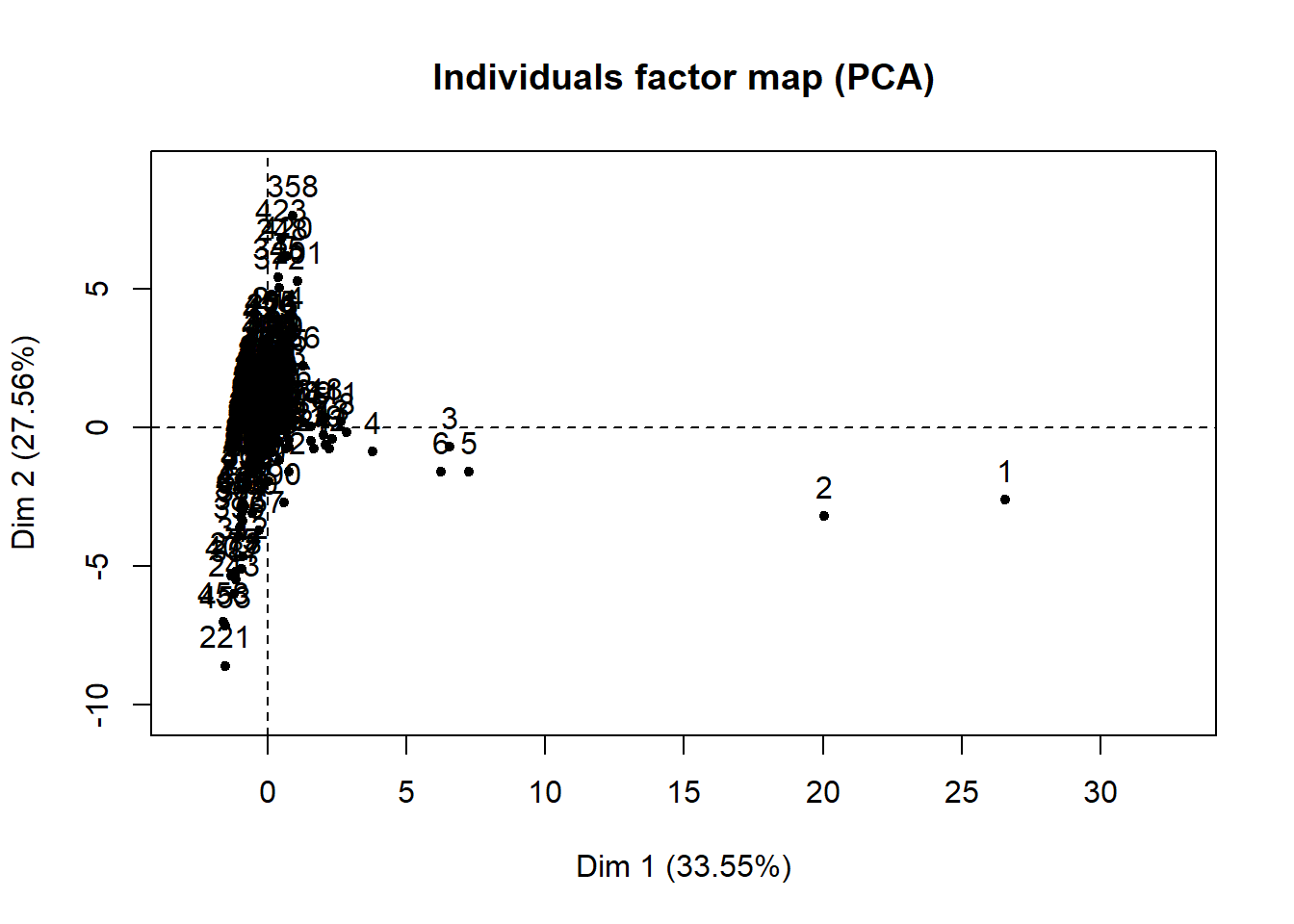
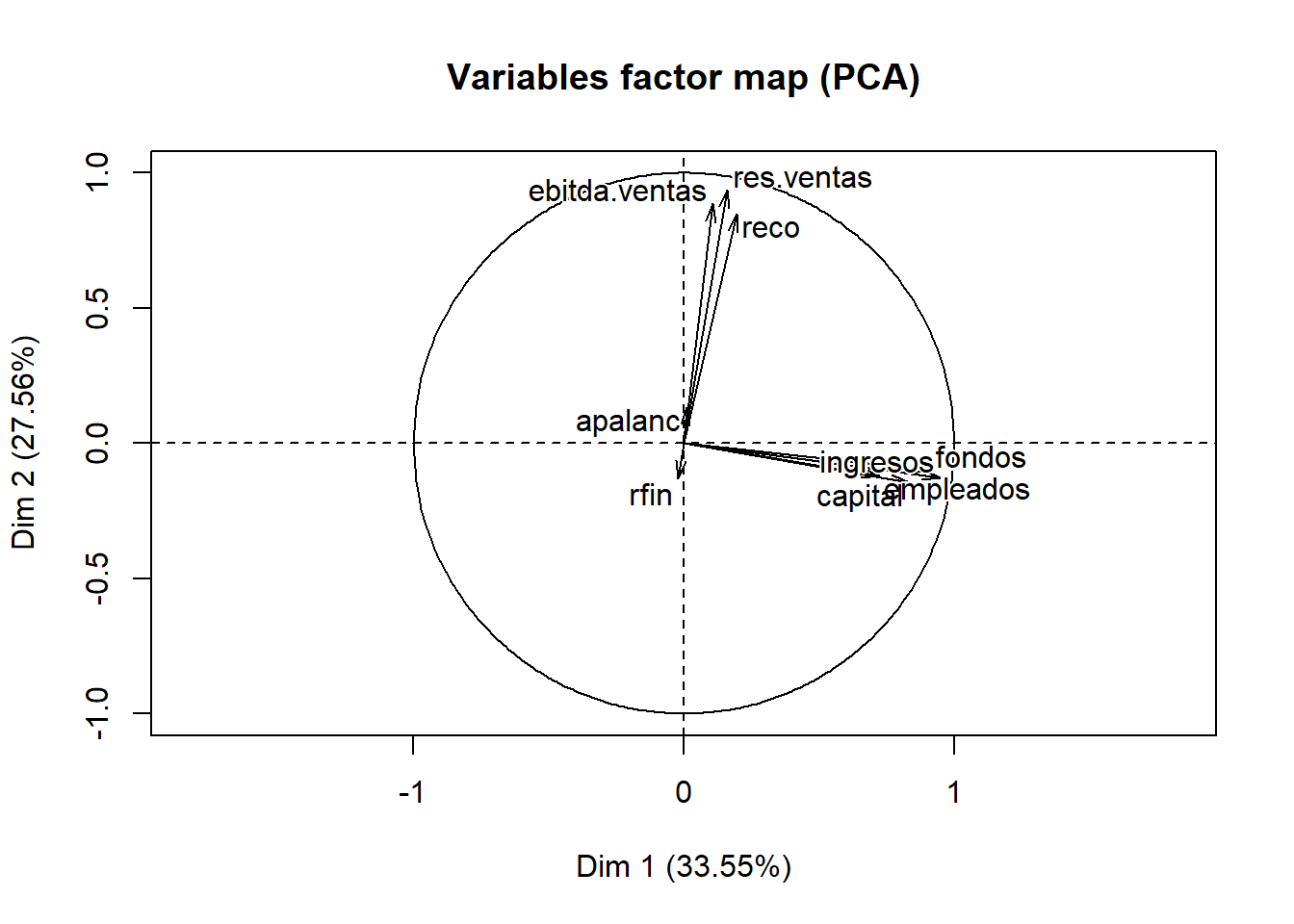
El objeto pca con el argumento ncp = 3 guarda solo la información relativa a las tres primeras dimensiones que se han determinado de interés.
Salvo que se especifique lo contrario (con el argumento graph = F), la función proporciona un gráfico de las puntuaciones de las empresas en el plano determinado por los dos componentes que explican mayor porcentaje de varianza, así como un gráfico de las cargas de las variables en esos componentes.
El objeto creado pca incluye información diversa:
pca## **Results for the Principal Component Analysis (PCA)**
## The analysis was performed on 459 individuals, described by 9 variables
## *The results are available in the following objects:
##
## name description
## 1 "$eig" "eigenvalues"
## 2 "$var" "results for the variables"
## 3 "$var$coord" "coord. for the variables"
## 4 "$var$cor" "correlations variables - dimensions"
## 5 "$var$cos2" "cos2 for the variables"
## 6 "$var$contrib" "contributions of the variables"
## 7 "$ind" "results for the individuals"
## 8 "$ind$coord" "coord. for the individuals"
## 9 "$ind$cos2" "cos2 for the individuals"
## 10 "$ind$contrib" "contributions of the individuals"
## 11 "$call" "summary statistics"
## 12 "$call$centre" "mean of the variables"
## 13 "$call$ecart.type" "standard error of the variables"
## 14 "$call$row.w" "weights for the individuals"
## 15 "$call$col.w" "weights for the variables"La información relativa al porcentaje de varianza explicada por cada componente puede encontrarse en pca$eig:
pca$eig## eigenvalue percentage of variance cumulative percentage of variance
## comp 1 3.01981357 33.5534841 33.55348
## comp 2 2.48024591 27.5582879 61.11177
## comp 3 1.87560196 20.8400217 81.95179
## comp 4 0.60329604 6.7032894 88.65508
## comp 5 0.40053809 4.4504232 93.10551
## comp 6 0.36376923 4.0418803 97.14739
## comp 7 0.12100680 1.3445200 98.49191
## comp 8 0.11563428 1.2848254 99.77673
## comp 9 0.02009411 0.2232679 100.00000Las cargas factoriales de las variables en pca$var$cor,
pca$var$cor## Dim.1 Dim.2 Dim.3
## apalanc 0.01138524 0.1334780 -0.960987296
## capital 0.83260118 -0.1453964 -0.006659214
## ebitda.ventas 0.10786497 0.8857966 0.092203289
## empleados 0.72173284 -0.1201506 -0.012877483
## fondos 0.90987017 -0.1003801 0.004370266
## ingresos 0.94904952 -0.1258779 -0.001442060
## reco 0.19654360 0.8473617 0.065362521
## rfin -0.02013154 -0.1302399 0.961410832
## res.ventas 0.16227352 0.9387822 0.121612199y la matriz de puntuaciones en pca$ind$coord,
head(pca$ind$coord)## Dim.1 Dim.2 Dim.3
## 1 26.560899 -2.6048220 0.16950893
## 2 20.037224 -3.1866039 -0.17313469
## 3 6.557825 -0.6872858 0.04424650
## 4 3.777499 -0.8692112 -0.02985954
## 5 7.269370 -1.5958065 -0.30924872
## 6 6.242442 -1.6076261 -0.17795085La información obtenida puede representarse también utilizando los gráficos mejorados que proporciona el paquete factoextra. A través de la función fviz_eig se puede representar el porcentaje de varianza explicada por cada componente:
factoextra::fviz_eig(pca, addlabels = TRUE)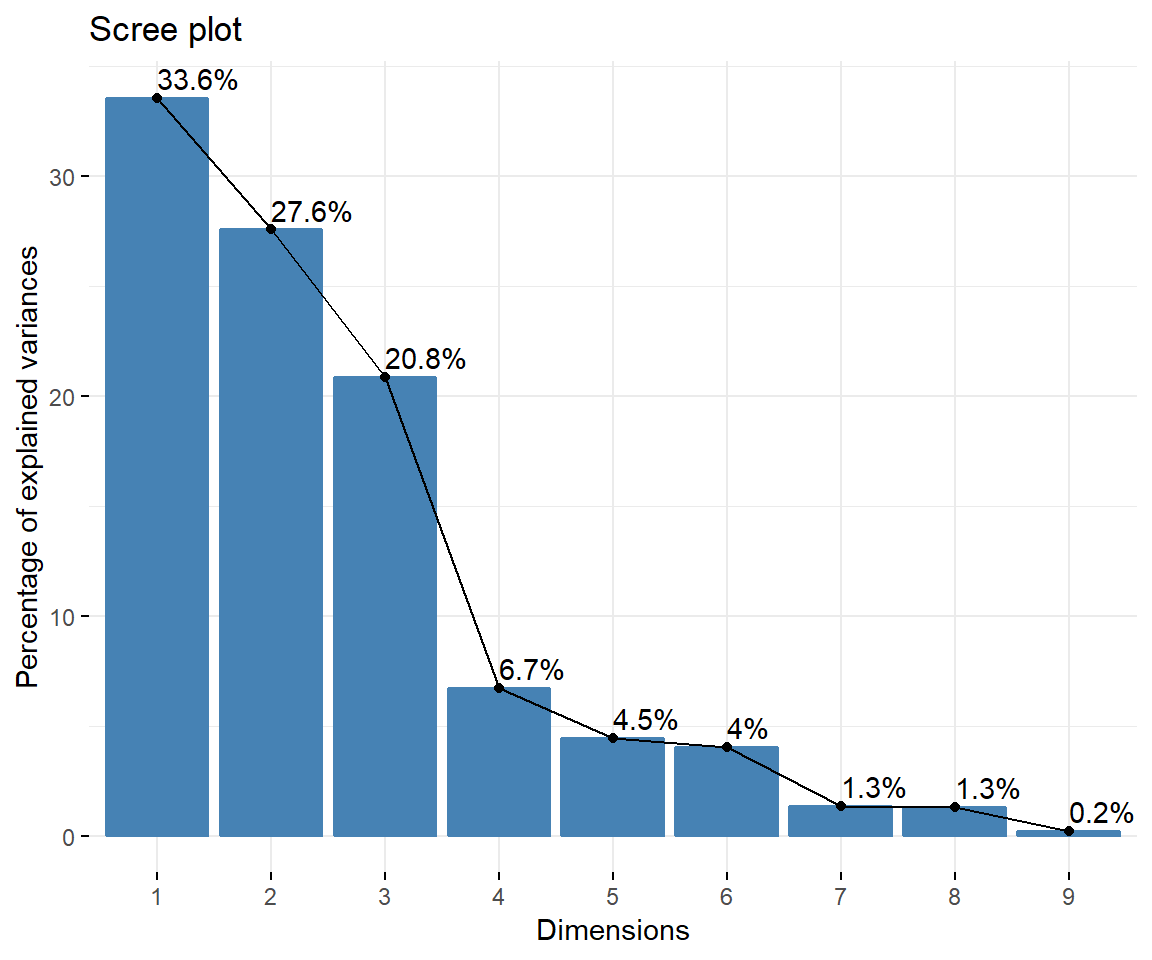
Y a través de la función fviz_pca_var las cargas factoriales:
factoextra::fviz_pca_var(pca,
col.var = "contrib", # Indica por colores el valor de las contribuciones
gradient.cols = c("green", "orange", "red"),
repel = TRUE) # Evita que se solapen los nombres de las variables
Mediante la función fviz_pca_biplot se representan las puntuaciones de las empresas y las cargas de las variables:
factoextra::fviz_pca_biplot(pca,
col.var = "contrib", # Indica por colores el valor de las contribuciones
gradient.cols = c("green", "orange", "red"))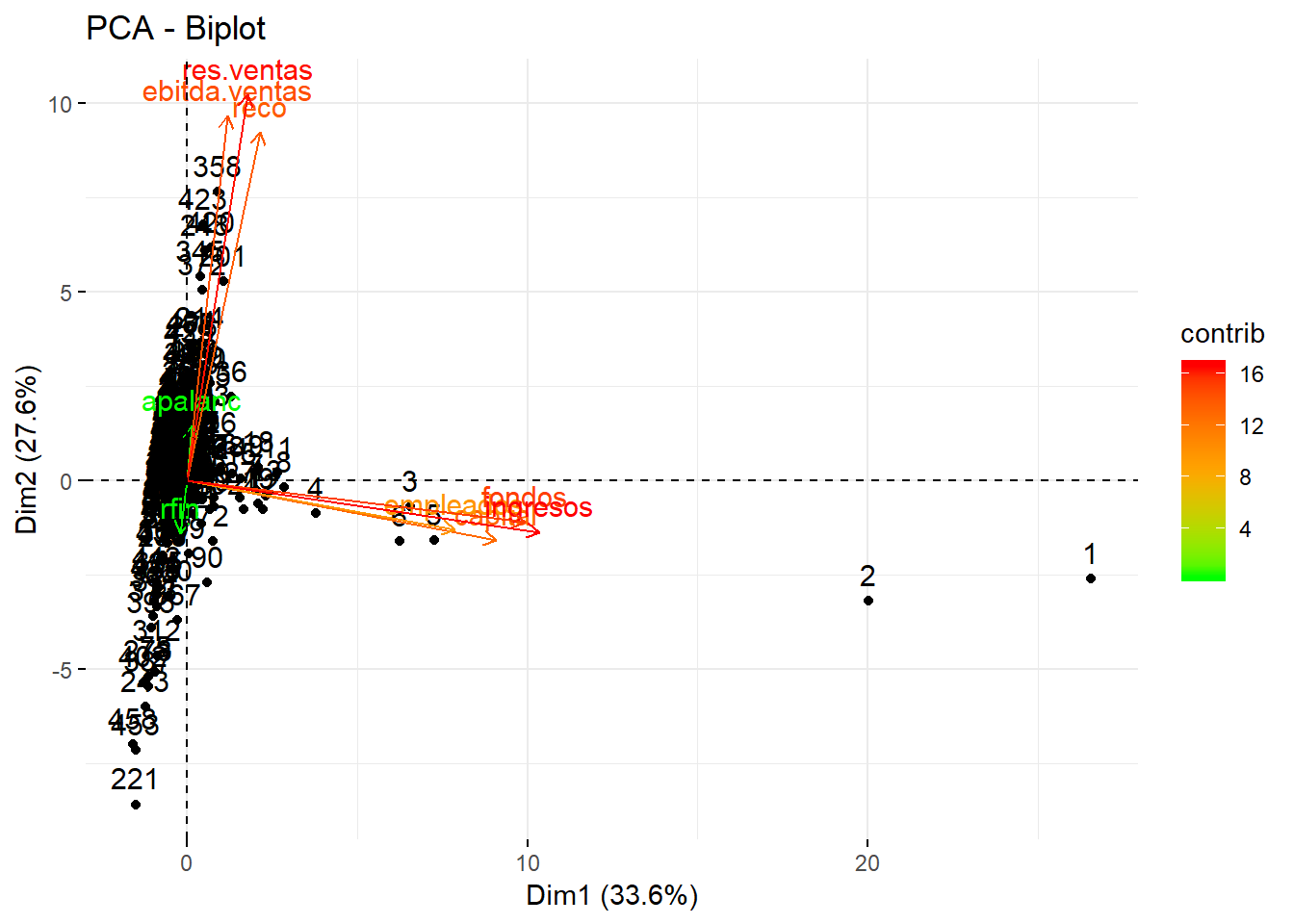
Finalmente, si se desea rotar la matriz de cargas proporcionada como salida por la función PCA con el método Varimax puede emplear la función varimax. Entre la información que proporciona esta salida se encuentran las cargas después de la rotación en cada una de las dimensiones.
rotado <- varimax(pca$var$cor)
rotado## $loadings
##
## Loadings:
## Dim.1 Dim.2 Dim.3
## apalanc -0.970
## capital 0.845
## ebitda.ventas 0.896
## empleados 0.732
## fondos 0.914
## ingresos 0.957
## reco 0.870
## rfin 0.970
## res.ventas 0.960
##
## Dim.1 Dim.2 Dim.3
## SS loadings 3.006 2.485 1.884
## Proportion Var 0.334 0.276 0.209
## Cumulative Var 0.334 0.610 0.820
##
## $rotmat
## [,1] [,2] [,3]
## [1,] 0.987344515 0.1581035 -0.01241297
## [2,] -0.158462254 0.9803805 -0.11723408
## [3,] -0.006365693 0.1177174 0.99302673Puede representar la información disponible acerca de las cargas en un par de componentes a través de la función plot con información adicional que haga que el gráfico sea similar a los que se obtienen por defecto con la función PCA. Por ejemplo, para los mismos dos componentes obtenidos en el apartado anterior (Comp.1 y Comp.2, ahora Dim.1 y Dim.2):
plot(rotado$loadings[,1], rotado$loadings[,2],
xlab = "Componente 1 (dim1)", ylab = "Componente 2 (dim2)", # Rótulos de los ejes
xlim = c(-1,1), ylim = c(-1,1), asp = 1, cex = 0.8, # Límites, aspecto y tamaño
pch = 20) # Tipo de símbolo
text(rotado$loadings[,1], rotado$loadings[,2],
labels = row.names(rotado$loadings), # Etiquetas de las variables
cex= 0.8) # Tamaño de letra
abline(v = 0, h = 0, lty = 3) # Ejes de coordenadas
symbols(0, 0, circles = 1, add = TRUE, inches = FALSE) # círculo de radio unidad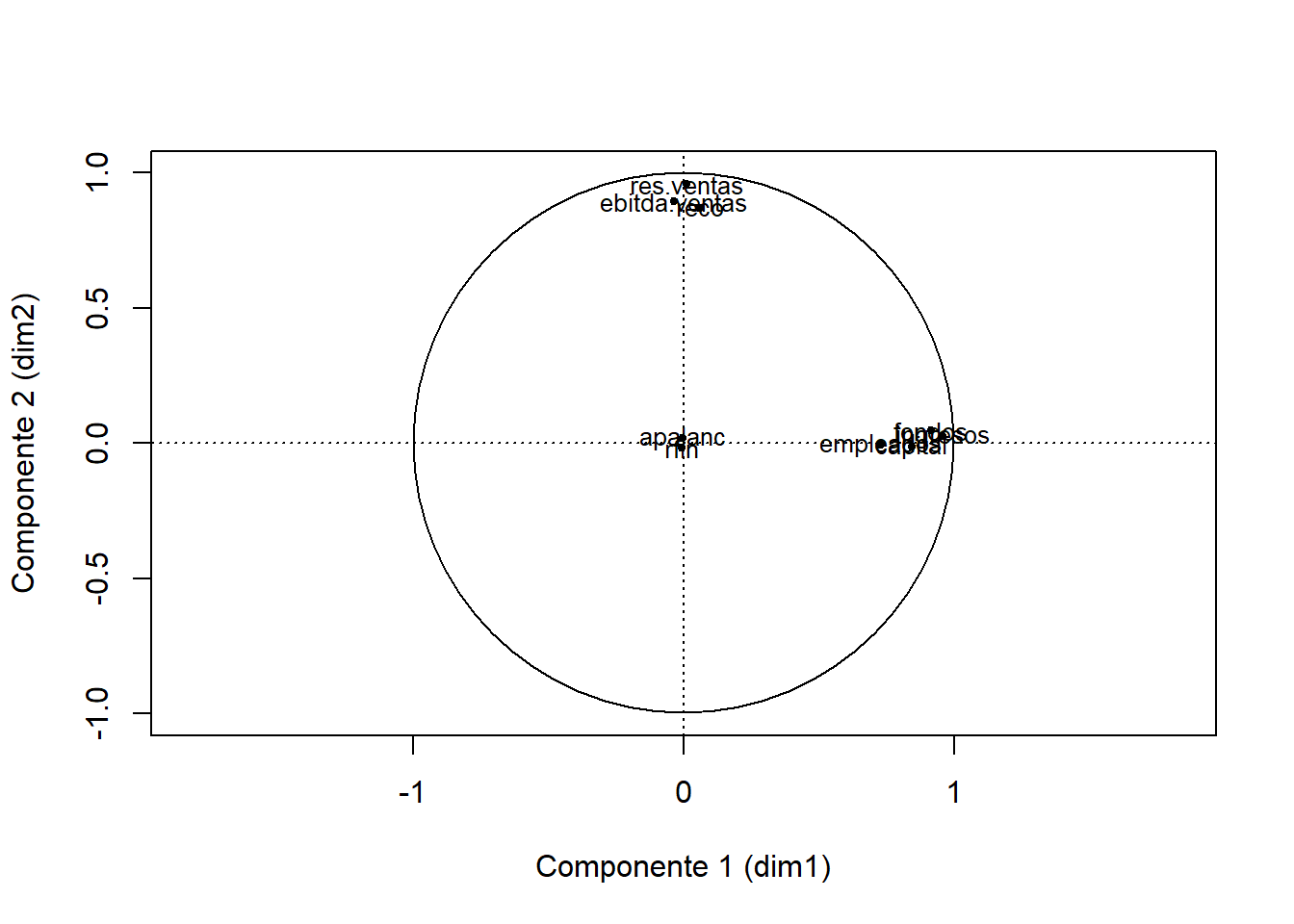
Para la obtención de las puntuaciones si emplea rotación puede multiplicar la salida correspondiente de la función PCA por la matriz de rotación que aparece en la salida de la función varimax:
matriz_nueva_rotada <- as.data.frame(pca$ind$coord %*% rotado$rotmat)
names(matriz_nueva_rotada) <- c("Comp.1", "Comp.2", "Comp.3")plot(matriz_nueva_rotada$Comp.1, matriz_nueva_rotada$Comp.2,
xlab = "Componente 1 (dim1)", ylab = "Componente 2 (dim2)", # Títulos de los ejes
pch = 20
)
text(matriz_nueva_rotada$Comp.1, matriz_nueva_rotada$Comp.2,
labels = row.names(matriz_nueva_rotada), # Etiquetas de las variables
cex= 0.8, pos = 3) # Tamaño de letra y posición de la etiqueta
abline(v = 0, h = 0, lty = 3)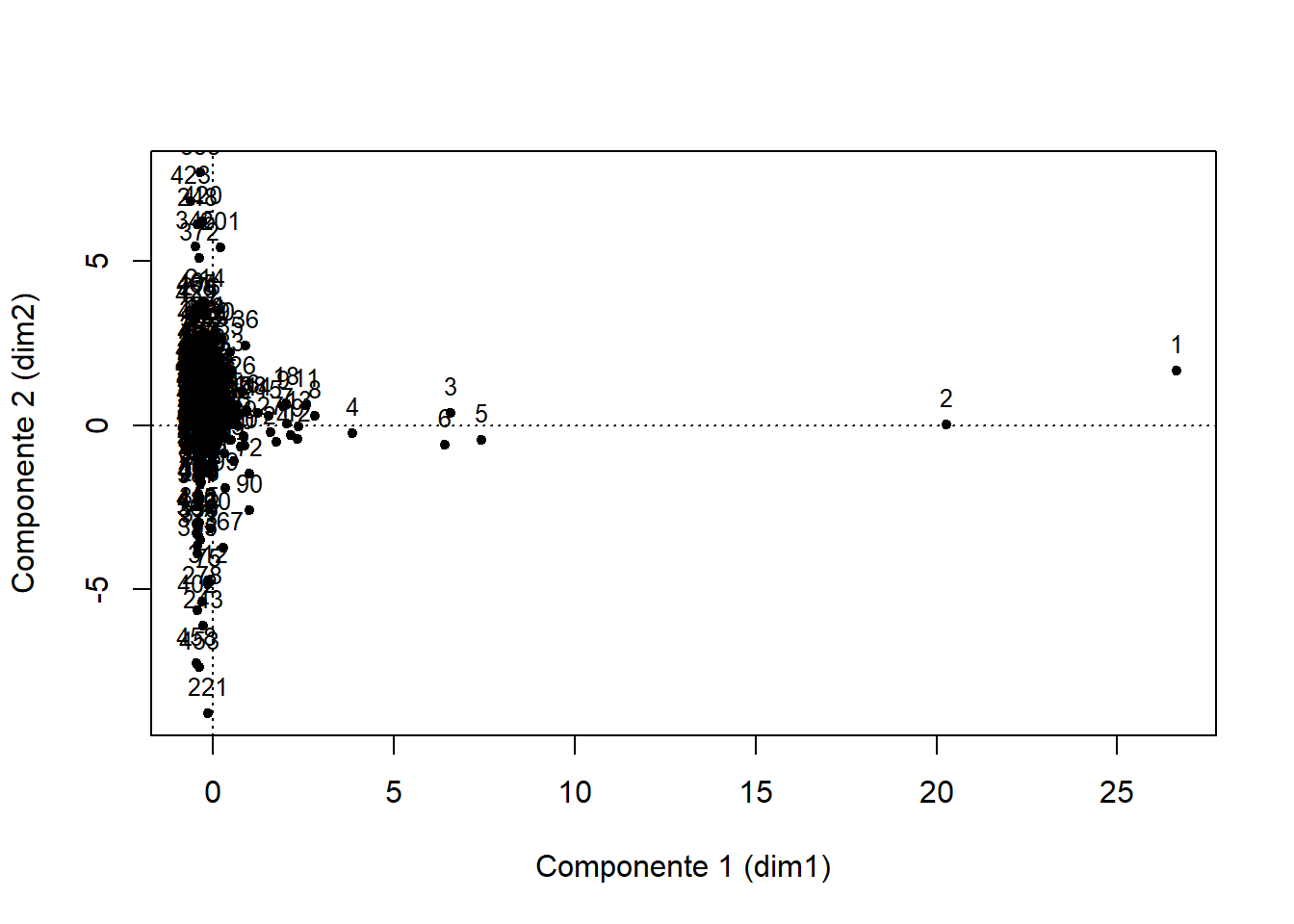
En el paquete Factoshiny se encuentran implementadas algunas aplicaciones shiny que facilitan el uso de las funciones del paquete FactoMineR. La función a utilizar para acceder a la aplicación shiny para realizar un análisis de componentes principales es PCAshiny. Su uso abre la aplicación en formato web, estando activa para trabajar mientras el usuario lo desee. La forma de acceder a la misma es:
Factoshiny::PCAshiny(datos)El código anterior tiene como resultado que se abra la siguiente página, desde la que puede interactuar, en su navegador:
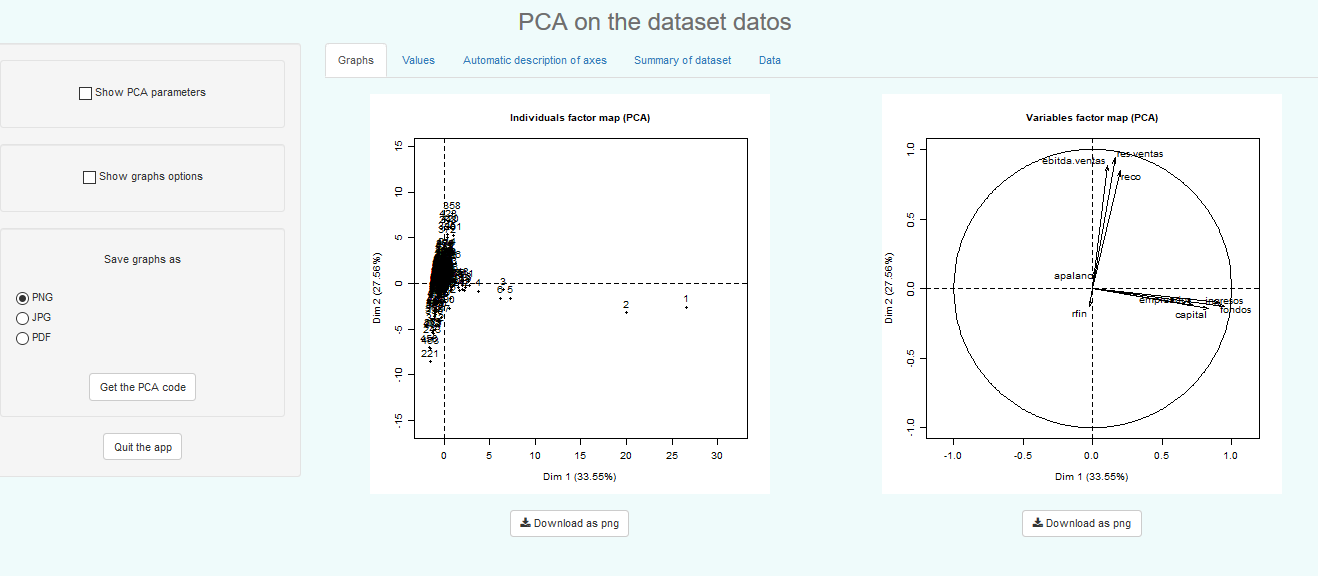
Observe que, para que funcione correctamente, debe estar cargado en la sesión el paquete FactoMineR, ya que se utiliza en estas aplicaciones. Recuerde que, para ello, debe utilizar
library("FactoMineR")
Grupo Innovación Docente: Estadística en Ciencias Sociales. Universidad de Murcia.
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.