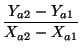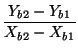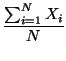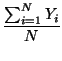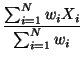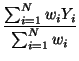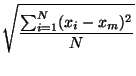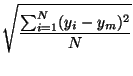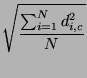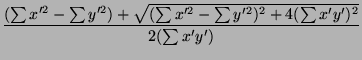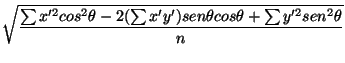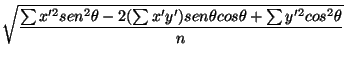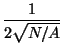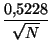Subsecciones
No resulta sencillo dar una definición de análisis espacial. En la bibliografía sobre SIG suelen mezclarse bajo este término una serie de herramientas bastante diferentes:
- Manipulación de datos espaciales, las herramientas básicas de gestión de un SIG
- Análisis descriptivo y exploratorio de datos espaciales
- Análisis estadístico inferencial de datos espaciales para determinar si los resultados del análisis descriptivo verifican determinadas hipótesis acerca de los datos
- Modelización espacial con el objeto de predecir la distribución espacial de los fenómenos estudiados
Siendo algo más restrictivos, el análisis espacial incluye un conjunto de herramientas que amplían las capacidades del análisis estadístico tradicional para abordar aquellos casos en los que la distribución espacial de los datos tiene influencia sobre las variables medidas y esta se considera relevante. La georreferenciación de los datos permite manejar un conjunto de conceptos nuevos como son los de distancia (entre dos puntos), adyacencia (entre dos polígonos o dos lineas), interacción y vecindad (entre puntos).
Aunque generalmente se incluye dentro del análisis espacial el estudio de variables espaciales, las herramientas utilizadas se han visto ya en los temas de álgebra de mapas e interpolación; por tanto el resto del tema se centrará en el análisis espacial de entidades:
- La distribución espacial de entidades puntuales
- Las relaciones entre entidades lineales interconectadas (redes)
- Las relaciones entre polígonos fronterizos
La mayor parte de las técnicas estadísticas básicas suponen graves problemas cuando intentamos aplicarlas a variables espacialmente distribuidas o medidas en individuos distribuidos en el espacio:
- Uno de los preceptos básicos de la estadística convencional es la independencia de los elementos que componen una muestra unos de otros. Al trabajar con datos espaciales este precepto no se cumple debido a la autocorrelación espacial. El resultado puede ser que los estadísticos resultantes aparezcan sesgados hacia los valores predominantes en los puntos muestreados. Un ejemplo extremo sería el de una tormenta de verano tan localizada que cayera entre los pluviómetros de la red del I.N.M. de manera que no se registrase nada de lluvia en estos. La precipitación media que se obtendría sería cero.
- Efectos de escala, los resultados pueden variar en función de la escala espacial con que se midan las variables. Por ejemplo la densidad de población varía si la medimos a escala 1:200000 (todo el poblamiento aparece agregado) o a escala 1:25000 (se tiene en cuenta la dispersión del poblamiento).
- Efectos de borde, muchas técnicas de análisis espacial fallan cuando aparecen fronteras al otro lado de las cuales los fenómenos son diferentes o no aparecen. Por ejemplo, si se hace un análisis del carácter agregado o disperso de los árboles en una isla, los ejemplares más cercanos a la costa tienen siempre menos árboles alrededor con lo que la distancia al más cercano será posiblemente mayor.
- Problema de la Unidad de Area Modificable, los resultados obtenidos a partir de valores agregados en unidades espaciales arbitrarias (por ejemplo unidades administrativas) van a depender de la configuración que adopten estas unidades35.
Prácticamente todos los cálculos que se llevan a cabo en un SIG vectorial se basan en la posición y las relaciones topológicas entre objetos:
- Distancia entre dos puntos, en casi todos los procedimientos de análisis espacial se incluye este concepto. Aunque se han definido varios tipos de distancia, se va a trabajar fundamentalmente con la distancia euclidiana por ser la más apropiada para la realidad espacial. La distancia entre los puntos i y j es tambien la longitud del segmento recto entre los puntos i y j (figura 85 A).
di, j = 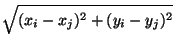
|
(50) |
- Area del trapecio situado bajo un segmento, se resuelve cómo la suma de las áreas del triángulo y el rectángulo bajo el segmento (figura 85 A)
Ati, i+1 = (xi+1 - xi)yi + 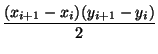 | = |(xi+1 - xi) | = |(xi+1 - xi)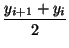
|
(51) |
Hay que tener en cuenta que el resultado será positivo si
xi+1 > xi y negativo en caso contrario. En este último caso el valor correcto es el valor absoluto de
Ati, i+1
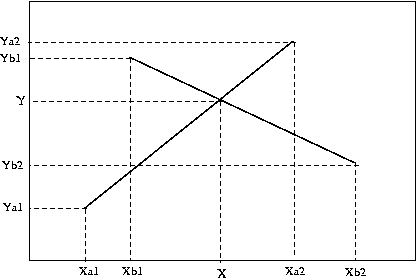
- Punto de corte de dos segmentos, es aquel que resulta de resolver el sistema de que forman las ecuaciones de la recta de ambos segmentos (figura 83):
| Ya = AXa + B |
|
|
(52) |
| Yb = CXb + D |
|
|
(53) |
donde
A = 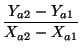 |
|
|
(54) |
| 1cmB = Ya1 |
|
|
(55) |
1cmC = 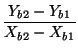 |
|
|
(56) |
| 1cmD = Yb1 |
|
|
(57) |
si el sistema tiene solución y el punto resultado forma parte de ambos segmentos, entonces la solución nos da el punto de corte (figura 83). En realidad el sistema tiene solución siempre, salvo que los segmentos sean paralelos, por lo que es necesario comprobar que la solución forme parte de ambos segmentos a la vez y sea, por tanto, su punto de corte. Es decir hay que comprobrar que X esté entre Xa1 y Xa2 y entre Xb1 y Xb2 y que Y esté entre Yb1 e Yb2 y entre Ya1 e Ya2.
Figura 83:
Punto de cruce entre dos segmentos
|
|
A partir de estas tres variables se puede obtener:
- Longitud (L) de una linea, es la suma de las distancias entre cada par de vértices consecutivos de la misma, asumiendo que la linea tiene N vértices:
L = 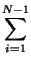 di, i+1 di, i+1
|
(58) |
- Distancia (D) en linea recta entre el inicio y el final de una linea: es decir entre su nodo inicial y su nodo final e índice de sinuosidad (Is)
| D = d1, N |
|
|
(59) |
| Is = L/D |
|
|
(60) |
- Perímetro de un polígono es la longitud de la linea que define el contorno del polígono.
- Longitud máxima del polígono puede definirse como la distancia máxima entre cualquier par de vértices en la linea que define el contorno del perímetro:
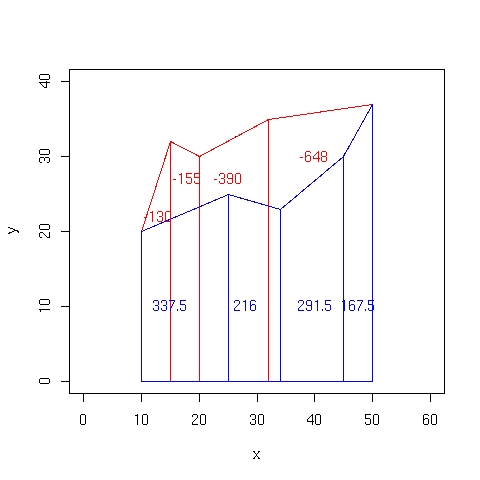
- Area de un polígono es el valor absoluto de la suma de todas las áreas de los trapecios bajo los segmentos que forman el polígono (figura 85):
A = |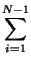 Ati, i+1| Ati, i+1|
|
(62) |
donde
Ati, i+1 es el area bajo el segmento formado por los vértices i e i + 1
En la figura 85 se aprecia como el perímetro del polígono genera una serie de trapecios cuyas áreas en metros cuadrados se indican en la figura y en la tabla 5. Los vertices se han contado en sentido contrario a las agujas del reloj, por lo que que los trapecios pintados de rojo tienen área negativa y los pintados de azul área positiva. La suma total da un valor de -310.5 por lo que el área del polígono será de 310.5 m2.
- A partir de área, perímetro y longitud máxima se han desarrollado diferentes índices de forma
Icompacidad = 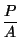 |
|
|
(63) |
Icircularidad = 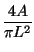 |
|
|
(64) |
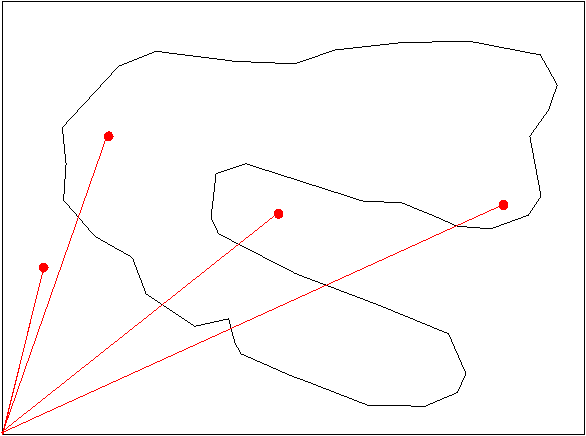
- Si se traza un segmento entre un punto y el origen de coordenadas y este segmento cruza un número impar de veces el límite de un polígono entonces está dentro del polígono si lo cruza un número par de veces está fuera del polígono (figura 84)
- Una linea intersecta a un polígono si alguno de sus segmentos tiene un punto de cruce con alguno de los segmentos del polígono.
- Dos polígonos se intersectan si sus perímetros se intersectan.
Figura 84:
Determinación de si un punto está dentro de un polígono
|
|
Figura 85:
Cálculo del área de un polígono
|
|
Tabla:
Resultados del cálculo del área del polígono (figura 85)
| i |
Área |
A. acumulada |
| 1 |
337.5 |
337.5 |
| 2 |
216 |
553.5 |
| 3 |
291.5 |
845 |
| 4 |
167.5 |
1012.5 |
| 5 |
-648 |
364.5 |
| 6 |
-390 |
-25.5 |
| 7 |
-155 |
-180.5 |
| 8 |
-130 |
-310.5 |
|
A continuación se van a presentar algunos casos de análisis de mapas de puntos, análisis de redes y geoestadística.
Se trata de capas de información en las que se registra la presencia de un conjunto de objetos puntuales (dolinas, individuos de una determinada especie, pozos, supermercados, etc.) en el espacio.
La primera cuestión que se plantea es analizar su distribución en el espacio. Para ello existen tres tipos de medidas:
- Las que, de forma similar a la estadística descriptiva clásica, calculan un conjunto de estadísticos de la distribución en el espacio (centro medio, desviación típica de distancias, etc.)
- Las que permiten calcular la densidad de puntos
- Las que buscan determinar el carácter agregado, distribuido o aleatorio de los objetos
Generalmente se asume como hipótesis nula que la distribución de puntos es aleatoria y como hipótesis alternativa que existe alguno de los siguientes efectos:
- Efecto de primer orden, la intensidad del proceso (frecuencia de aparición de puntos) es mayor en unas partes del área de estudio que en otras.
- Efecto de segundo orden, la aparición de un punto incrementa la probabilidad de que aparezcan otros en las cercanias.
Si una distribución de puntos no experimenta efecto de primer orden se dice que estacionaria de primer orden y si no experimenta el efecto de segundo orden se dice que es estacionaria de segundo orden. No siempre es fácil distinguir entre los efectos de primer y segundo orden.
Para que un conjunto de puntos sea considerada una distribución de puntos y se le pueda aplicar el conjunto de técnicas que van a explorarse a continuación, se requiere que cumpla una serie de condiciones:
- El área de estudio debe determinarse de forma objetiva
- El conjunto de puntos debe corresponder a la población completa y no a una muestra
- Las coordenadas de cada punto deben corresponder exactamente a la ubicación del punto (no pueden ser centroides o coordenadas medias)
Las medidas de centralidad son los centro medio, mediano y modal, que se calculan como el punto definido por los valores medio, mediano y moda de las coordenadas X e Y de la muestra.
Xm = 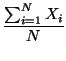 |
|
|
(65) |
Ym = 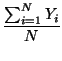 |
|
|
(66) |
Dependiendo del tipo de distribución que tengan los valores de X e Y, será más correcta la utilización del centro medio o mediano como estadístico de centralidad.
En el caso de que los puntos tengan asociada una variable (por ejemplo altura de los arboles). Puede calcularse un centro ponderado utilizando esta variable como factor de ponderación:
Xwm = 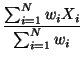 |
|
|
(67) |
Ywm = 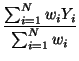 |
|
|
(68) |
donde w representa una variable, normalmente no espacial, medida en cada punto. Por ejemplo, los puntos pueden ser nucleos urbanos y w su población.
Respecto a la dispersión, puede utilizarse el equivalente a la desviación típica igual que antes se han utilizado los equivalentes a la media:
Puede obtenerse tambien la desviación típica de las distancias como la raiz cuadrada de la media de los cuadrados de las distancias al punto medio:
 = = 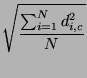 |
|
|
(71) |
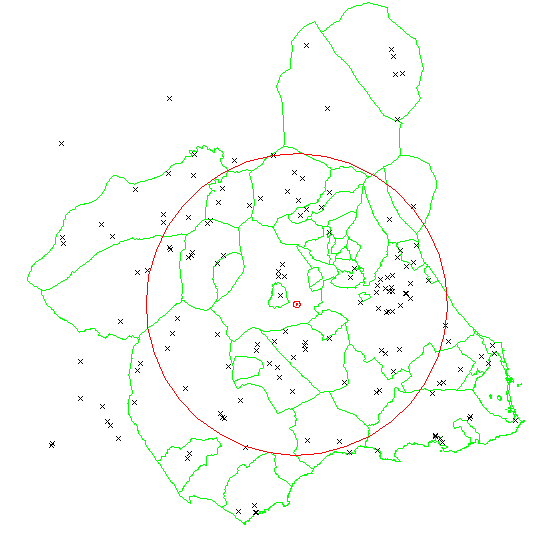
En la figura 86 aparece el punto medio y el círculo de una desviación típica de distancias del mapa de observatorios meteorológicos de la cuenca del Segura. De un modo similar pueden derivarse ecuaciones para calcular la desviación típica ponderada.
Figura 86:
Punto central y circunferencia de desviación típica
|
|
Todos los métodos vistos hasta el momento, asumen que la distribución es isótropa, es decir que las desviaciones son iguales en cualquier dirección y que la desviación típica puede asimilarse de este modo al radio de una circunferencia.
En realidad esto no suele ocurrir así sino que hay una dirección a lo largo de la cual la variabilidad es menor y otra, generalmente perpendicular, con mayor variabilidad. Piensa por ejemplo en la distribución de humedad del suelo en un valle alargado, la dirección del valle establece el eje de menor variabilidad. En estos casos se dice que la variable es anisotrópica.
El eje de mayor variabilidad pueden obtenerse mediante la ecuación:
tan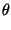 = = 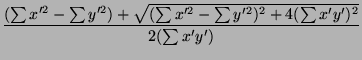
|
(72) |
donde x' = x - Xm, y = y - Xm y 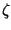 es el ángulo formado por el eje de máxima variabilidad y'' respecto al eje y'. El eje de mínima variabilidad x'' será por tanto perpendicular a y''.
es el ángulo formado por el eje de máxima variabilidad y'' respecto al eje y'. El eje de mínima variabilidad x'' será por tanto perpendicular a y''.
Las desviaciones de las distancias respecto a x'' e y'' vienen dadas por:
En ocasiones interesa obtener una medida de la disposición de los puntos unos respecto a otros, tratando de identificar estructuras concentradas o dispersas. Muchos fenómenos que tienen una manifestación espacial tienden a aproximarse a algunos de estos extremos.
Varias son las técnicas que nos proporcionan una medida del grado de dispersión o concentración de las observaciones puntuales en un área. A continuación se expone una técnica de uso frecuente en la investigación de fenómenos espaciales: el análisis del vecino más próximo. Otras técnicas como el test de 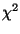 o el test de Kolmogorov-Smirnov pueden consultarse en la bibliografía.
o el test de Kolmogorov-Smirnov pueden consultarse en la bibliografía.
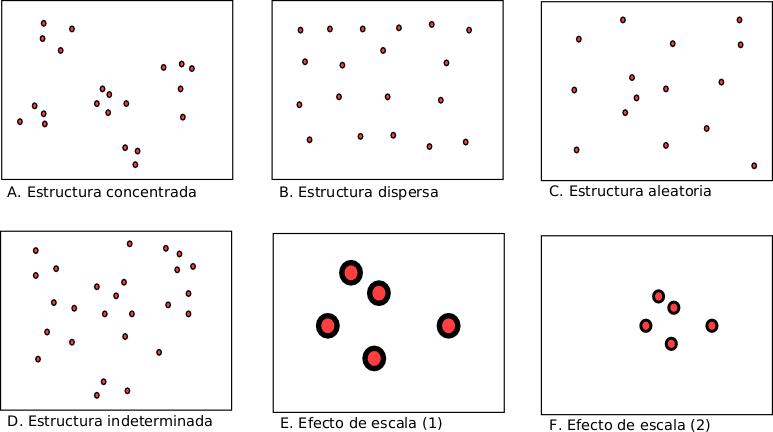
Este tipo de análisis de vecindad se fundamenta en el reconocimientos de tres tipos de estructuras puntuales:
- concentrada, con una elevada densidad de puntos en zonas concretas del área de estudio (figura 87 A)
- dispersa, los puntos tienden a ocupar la mayor parte del área de estudio maximizando la distancia entre los puntos (figura 87 B)
- aleatoria, establecida al azar (figura 87 C)
En muchos casos el tipo de estructura no será tan evidente como en los tres primeros esquemas de la figura 87 sino que aparecerán casos del tipo de la figura 87, en estos casos es necesario llevar a cabo un test estadístico para verificar cual es el tipo de distribución.
Pero también hay que tener en cuenta la existencia de problemas de escala. La figura 87.E presenta un zoom realizado sobre la 87.A, la aplicación del test del vecino más próximo a este caso daría como resultado una estructura aleatoria ya que el muestreo no se ha hecho a la escala adecuada. El tamaño del área de estudio también afecta a los resultados, la figura 87.F representa el caso anterior pero ahora ampliando el rectángulo que contiene los puntos, en este caso el test del vecino más próximo daría como resultado una estructura concentrada.
Figura 87:
Estructuras de agrupameniento de fenómenos puntuales
|
|
Se parte del cálculo para cada punto de su distancia al vecino más próximo d1, posteriormente se calcula la media de estas distancias d1m y se compara con la media que se obtendría de una distribución al azar d1a.
d1a = 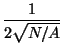
|
(75) |
R1 = 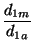
|
(76) |
donde N es el número de puntos y A el tamaño del área de trabajo. No debe olvidarse que estamos calculando la distribución de puntos dentro de un área de estudio cuya extensión no siempre está claramente establecida a priori y va a tener una influencia decisiva en el resultado final. Si se tienen unos límites definidos (un municipio, una cuenca hidrográfica) no hay problemas, pero los límites irregulares y posiblemente arbitrarios que impone una pantalla de ordenador pueden afectar al resultado del índice.
Si R1 = 1, ambas distribuciones son idénticas y nos encontraríamos ante una estructura puramente aleatoria. Si R1 se aproxima a 0 significa que las distancias observadas son pequeñas y por tanto la estructura es concentrada. El valor máximo de R1 es 2.149, e indicaría una estructura netamente dispersa.
Rara vez van a aparecer estos valores extremos sino que obtendremos valores intermedios. En realidad la aleatoriedad no vendría dada exclusivamente por R1 = 1 sino por una banda de valores alrededor de 1. Los límites de esta banda vienen dados por los valores críticos de R1:
R1c = 1±z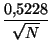
|
(77) |
donde z depende del nivel de significación escogido (tabla 47.3.2), el nivel de significación indica las probabilidades que asumimos de equivocarnos si aceptamos que la distribución no es aleatoria. Un valor de 0.05 implica, por ejemplo, que existe un 95% de probabilidades de que no nos equivoquemos en el diagnóstico.
Tabla 6:
Valores de z para diferentes niveles de significación
| Nivel de |
Valor z |
| significación |
|
| 0.05 |
1.645 |
| 0.01 |
2.326 |
| 0.005 |
2.576 |
| 0.001 |
3.090 |
|
|
|
Si
1 - z*0.5228*N-0.5 < R1 < 1 + z*0.5228*N-0.5 se asume por tanto que la distribución es al azar, sin concentración ni dispersión.
Si
R1 < 1 - z*0.5228*N-0.5 la distribución es concentrada y si
R1 > 1 + z*0.5228*N-0.5 se considera que es dispersa.
alonso
2006-02-13
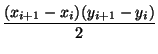 | = |(xi+1 - xi)
| = |(xi+1 - xi)