Sea tn el instante en que se produce la n-ésima salida del sistema.
Justo después de tn, sea Nn
el número de clientes en el sistema. Son variables aleatorias con
valores enteros (y no negativos): ![]() es un proceso estocástico en tiempo discreto.
es un proceso estocástico en tiempo discreto.
Si existe el estado estacionario, entonces existirá
N es el número de clientes tras una salida en estado estacionario. Se pretende calcular E(N).
Entonces
siendo A el número de llegadas al sistema en S unidades de tiempo (A también es v.a.) y
Sabiendo que S=s, entonces ![]() .
Además, usaremos la notación
.
Además, usaremos la notación ![]() .
.
El estado estacionario existe si ![]() .
.
Como Nn+1 = Nn + A - Un, tomando esperanzas:
Y tomando límites:
(Probabilidad de que queden clientes en el sistema tras una salida en estado estacionario)
Ahora, como paso previo para el cálculo de E(N), interesa determinar P(Nn+1=j|Nn=i).
Es obvio que P(Nn+1=j|Nn=i)=0
si ![]() .
Basta ahora considerar
.
Basta ahora considerar ![]() .
.
Caso 1: ![]() .
.
![]()
![]()
Este valor no depende de n: son probabilidades estacionarias (sólo dependen del estdo del sistema). Vienen en función de la diferencia j-i. Lo llamaremos kj-i+1 .
Una vez conocida la distribución de S, ya se puede determinar el valor anterior.
Caso 2: ![]() .
.
Razonando como antes, pero teniendo en cuenta que en esta ocasión deben llegar j:
Éste es el valor que toma kj .
Calculemos ahora E(N). Se parte de
Elevamos al cuadrado y tomamos esperanzas:
Ahora se observa que por definición de Un es E(Un2)=E(Un) y E(NnUn)=E(Nn). Además, A y Nn son independientes (el proceso de llegadas y el proceso de salidas son independientes). De igual modo, A y Un son independientes.
Tomando límites en n y usando ![]() :
:
Como ![]() ,
basta conocer Var(A).
,
basta conocer Var(A).
Para su cálculo se necesita de estos resultados previos:
y teniendo en cuenta que la variable (A|S=s) sigue una distribución ![]() ,
se tiene:
,
se tiene:
Así
Finalmente, calculemos P(N=n). Sea Pj=P(N=j).
Por el teorema de la probabiliad total,
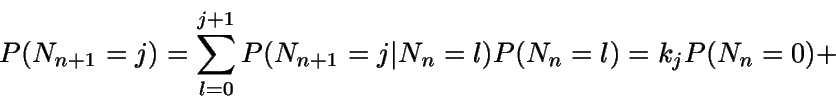
Al tomar límites en n:
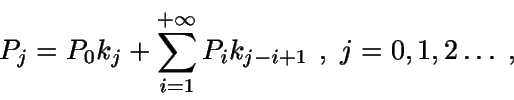
siendo kl=0 si l<0.
En notación matricial:
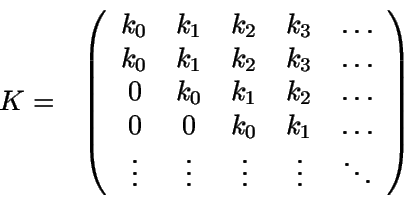
La entrada (i,j) representa la probabilidad de pasar del estado i al estado j en estado estacionario.
Si P=PK para cierto ![]() ,
entonces existirá el estado estacionario.
,
entonces existirá el estado estacionario.
Las entradas de P vienen dadas por
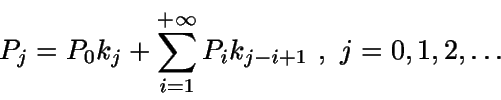
Multiplicando por sj+1 la j-ésima ecuación:
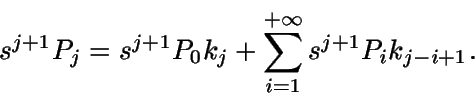
Sumando todas las igualdades obtenidas (y representado por G la función generatriz de probabilidades de N):
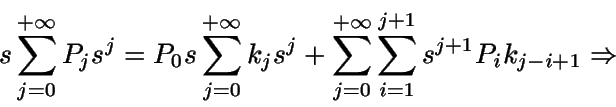
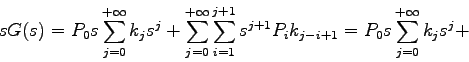
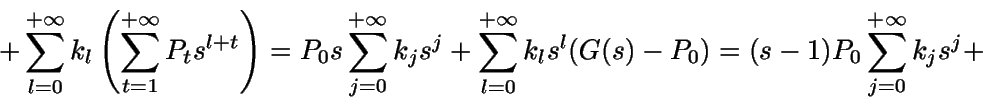
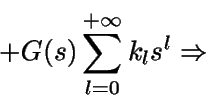
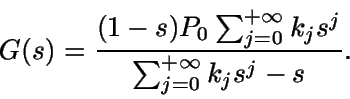
Como G(1)=1, utilizando la regla de l'Hôpital se tiene
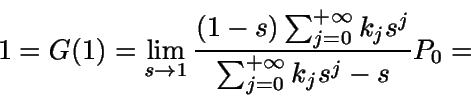
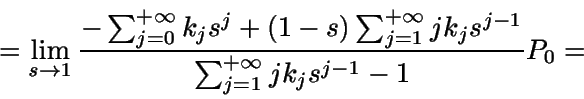
Caso particular: El modelo M/D/1
Los tiempos de servicio son constantes: ![]() .
.
![]()
kj = P(haya j llegadas en ![]() unidades de tiempo) =
unidades de tiempo) =
![]()
Ahora
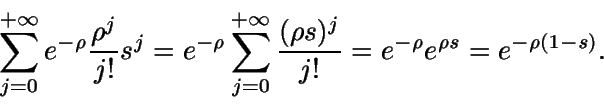
Luego
Como
entonces
Así que
![\begin{displaymath}P_n= (1-\rho) \sum_{i=1}^n (-1)^{n-i} e^{i\rho} \left [\fra......)!} + \sum_{n-i-1>0}\frac{(i\rho)^{n-i-1}}{(n-i-1)!} \right].\end{displaymath}](img294.gif)
Caso particular: el modelo M/M/1
Los tiempos de servicio son ![]() .
.
![]()
![]()
(Distribución geométrica) Ahora
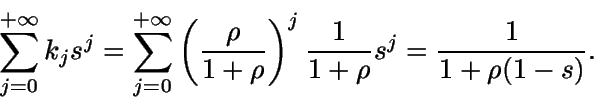
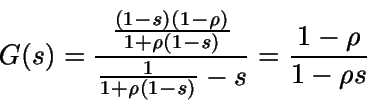
Función generatriz de una distribución geométrica)
Así