Comportamiento transitorio de M/M/1/1

Sea N(t) el número de clientes en el sistema en el instante t. Sean

P₀(t)=P(N(t)=0)

y

P₁(t)=P(N(t)=1)=1-P₀(t).

Se tiene que $P_0(t)+P_1(t)=1, \ N(t) \in \{0,1\} \ \forall t \geq 0$.

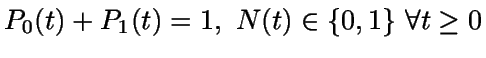Determinemos ahora las ecuaciones que rigen el sistema:

$$\left \{ \begin {array}{ccc} P_0(t+h) & = & P_0(t)(1-\lamb... ...ambda h + o(h)) + P_1(t) (1-\mu h + o(h)) \end{array} \right.$$

$$\left \{ \begin {array}{ccc} P_0'(t) & = & -\lambda P_0(t)... ...P_1'(t) & = & \lambda P_0(t) - \mu P_1(t) \end{array} \right.$$

Ambas ecuaciones son equivalentes.

$$P_0'(t) = -\lambda P_0(t) + \mu (1-P_0(t)) = -(\lambda + \mu) P_0(t) + \mu\Rightarrow$$

$$P_0'(t) + (\lambda + \mu) P_0(t) = \mu\Rightarrow$$

$$P_0(t) = e^{-(\lambda + \mu)t} \left ( \int {e^{(\lambda + \m... ...t ( \frac{\mu}{\lambda + \mu} e^{(\lambda+\mu)t} + c \right) =$$

$$= \frac {1}{1+\rho} + c e^{-(\lambda+\mu)t}.$$

Evaluando en t=0:

$$P_0(0)=\frac{1}{1+\rho} +c \quad; \quad c=P_0(0) - \frac{1}{1+\rho},$$

luego

$$P_0(t)= \frac{1}{1+\rho} + \left ( P_0(0) - \frac{1}{1+\rho} \right ) e^{-(\lambda + \mu) t}.$$

Si el sistema está inicialmente vacío, entonces P₀(0)=1.

Si t tiende hacia infinito, entonces

$$P_0= \frac{\mu}{\lambda + \mu} \quad , \quad P_1=\frac{1}{1+\rho}.$$

Por lo tanto, se alcanza el estado estacionario independientemente de lo que valga 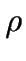$\rho$.