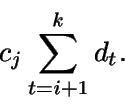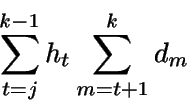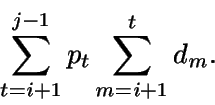Siguiente: Modelo 8 Nivel anterior: Modelos de inventario con revisión periódica Previa: Modelos de inventario con revisión periódica

Modelo 7

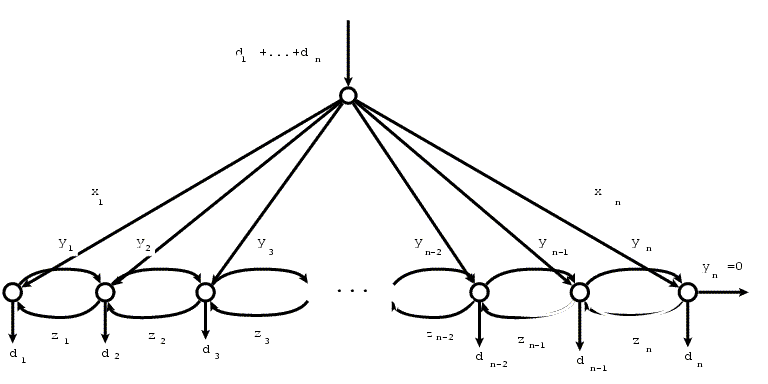
Se conoce la demanda de cada período, pero no como está distribuida en él.
Demanda d_t durante el t-ésimo período.
Escasez permitida: coste p_t por unidad de inventario negativo al final del t-ésimo período.
Coste de material: c_t x_t en el período t.
Coste de almacenamiento: h_t por unidad de inventario positivo al final del t-ésimo período.
Política 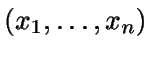$(x_1,\dots,x_n)$ : debe determinarse la cantidad x_t que se pide al inicio del período t-ésimo a coste total mínimo y de modo que Y_n=0.

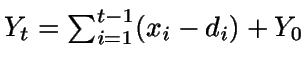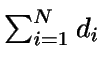Se tiene que $Y_t = \sum_{i=1}^{t-1} (x_i-d_i) + Y_0$ . El problema se resuelve usando programación dinámica. Sabemos que la demanda total es $\sum_{i=1}^N d_i$ . Como las funciones de coste son cóncavas (en particular, lineales), existe un flujo extremo (sólo entra flujo en cada nodo por un arco).

El grafo queda particionado en subgrupos de nodos (adyacentes entre sí en cada grupo), realizándose un solo pedido en cada subgrupo.

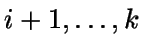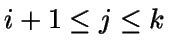Sea c_ijk el coste de suministrar la demanda de los períodos $i+1,\dots,k$ haciendo un pedido al principio del período j-ésimo, $i+1 \leq j \leq k$ .

Coste de material para este subgrupo:

$\begin{displaymath}c_j \sum_{t=i+1}^k d_t.\end{displaymath}$

Coste de almacenamiento para este subgrupo:

$\begin{displaymath}\sum_{t=j}^{k-1} h_t \sum_{m=t+1}^k d_m\end{displaymath}$

Coste de escasez para este subgrupo:

$\begin{displaymath}\sum_{t=i+1}^{j-1} p_t \sum_{m=i+1}^t d_m.\end{displaymath}$

Así

$\begin{displaymath}c_{ijk} = c_j \sum_{t=i+1}^k d_t + \sum_{t=j}^{k-1} h_t \sum_{m=t+1}^k d_m + \sum_{t=i+1}^{j-1} p_t \sum_{m=i+1}^t d_m.\end{displaymath}$

Sea ahora

$\begin{displaymath}c_{ik} = \text{\, mín \,} \{c_{ijk} \}_{i+1 \leq j\leq k}.\end{displaymath}$

Sea f_i el coste mínimo del subproblema que sólo incluye los períodos i+1, ..., n. El óptimo de nuestro problema será f₀.

$\begin{displaymath}\begin{array}{ccc} f_n & = & 0, \\ f_{n-1} & = & c_{n-1,n}. \end{array}\end{displaymath}$

Se tiene la recurrencia

$\begin{displaymath}f_i = \text{ \, mín \,} \{f_k+c_{ik} \}_{i+1\leq k \leq n}.\end{displaymath}$