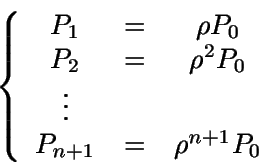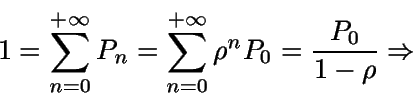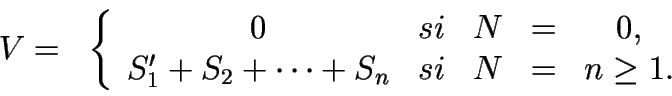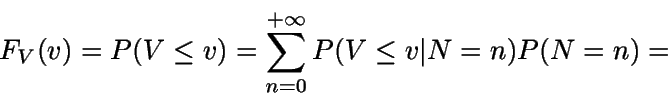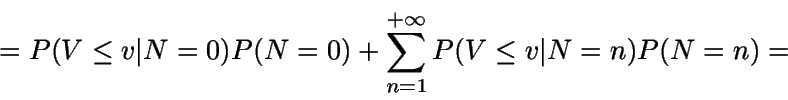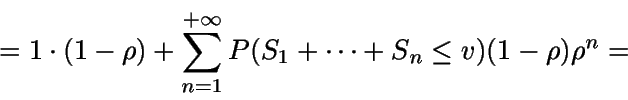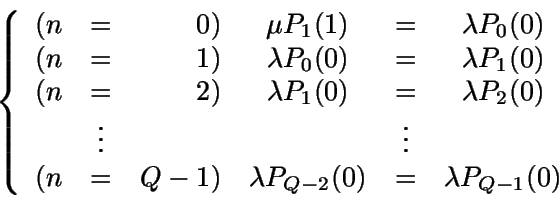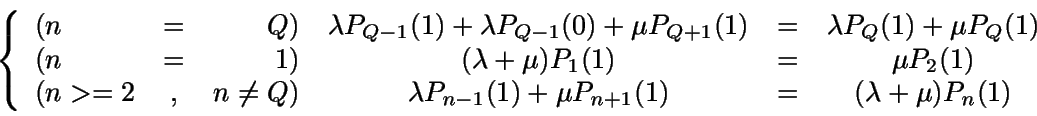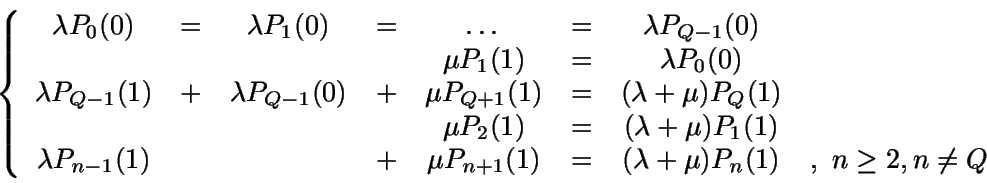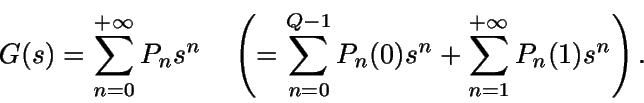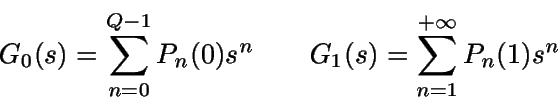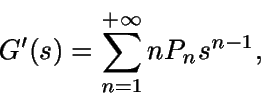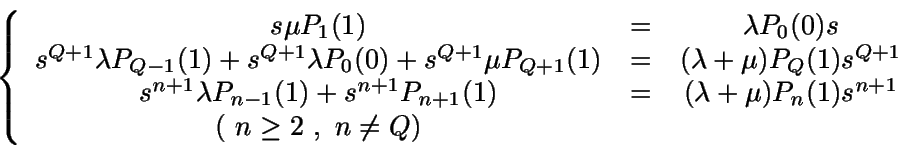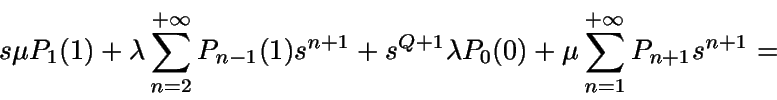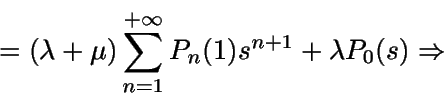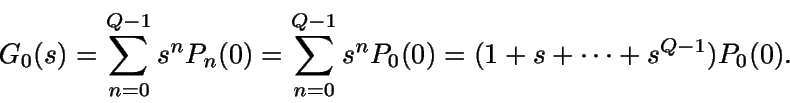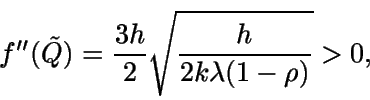Siguiente:El
sistema M/M/1/kNivel anterior:Modelos
de colas estocásticosPrevia:Modelos
de colas estocásticos
El modelo M/M/1
En primer lugar, se describe el modelo:
-
1.
-
 :
El proceso de llegadas es de Poisson homógeneo con tasa
:
El proceso de llegadas es de Poisson homógeneo con tasa  .
.
Sea T la variable aleatoria que representa el tiempo entre dos llegadas
consecutivas.
Sea t>0 y representemos por n(t) el número de llegadas al sistema
hasta el instante t.
Como los incrementos son independientes:
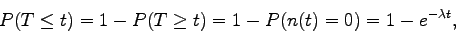
luego 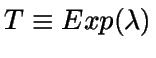 .
Recíprocamente, se tiene el siguiente resultado:
.
Recíprocamente, se tiene el siguiente resultado:
Si 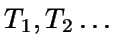 son independientes, siendo Ti el tiempo transcurrido
entre las llegadas (i-1)-ésima e i-ésima, todas ellas con
distribución
son independientes, siendo Ti el tiempo transcurrido
entre las llegadas (i-1)-ésima e i-ésima, todas ellas con
distribución 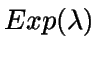 ,
entonces
,
entonces 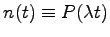 .
.
Demostración:
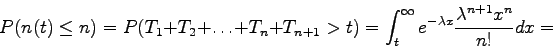
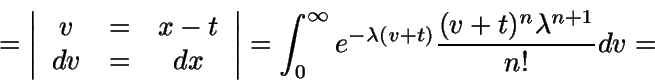
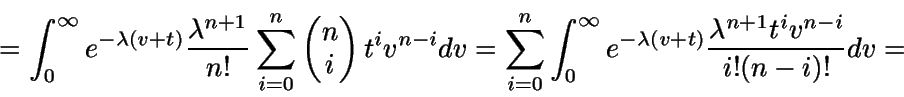
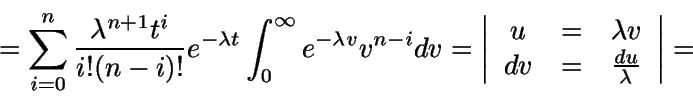
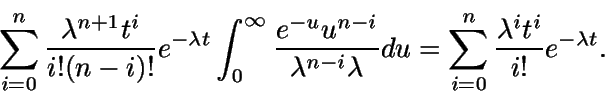
(El último paso se hace considerando la expresión
de la función gamma)
-
2.
-
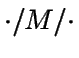 :
Siempre que el servidor esté ocupado, el proceso de salida es de
Poisson homogéneo de tasa
:
Siempre que el servidor esté ocupado, el proceso de salida es de
Poisson homogéneo de tasa 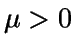 .
.
Razonando como antes, se tiene que los tiempos de servicio son 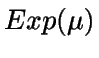 .
.
-
3.
-
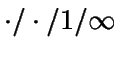 :
El sistema tiene un único servidor y capacidad infinita.
:
El sistema tiene un único servidor y capacidad infinita.
Se trata de un proceso de nacimiento y muerte con tasa de nacimiento 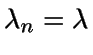 ,
,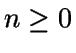 y tasa de muerte
y tasa de muerte 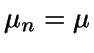 ,
,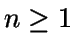 .
.
Debe observarse que la distribución exponencial tiene ausencia
de memoria, es decir, si 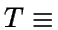 Exp(
Exp(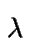 ),
entonces
),
entonces
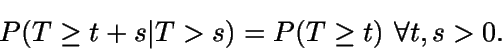
La demostración de esta propiedad es inmediata observando
la
expresión de la función de distribución asociada.
Ahora se puede proceder a analizar el comportamiento del sistema. Se
define la intensidad del tráfico como
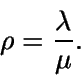
Si 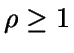 ,
no se alcanza el estado estacionario, mientras que si
,
no se alcanza el estado estacionario, mientras que si 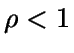 ,
entonces sí que se llega a este estado.
,
entonces sí que se llega a este estado.
Sea Pn(t)=P(N(t)=n)
la probabilidad de que en el instante t haya n clientes en el sistema.
Yendo a las ecuaciones que se obtuvieron para un proceso de nacimiento
y muerte, tenenos que
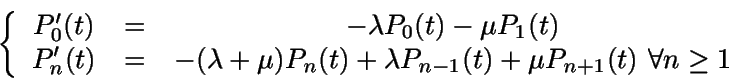
En el estado estacionario (a partir de aquí suponemos ya 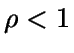 )
se tiene el siguiente sistema, denominado ecuaciones de equilibrio:
)
se tiene el siguiente sistema, denominado ecuaciones de equilibrio:
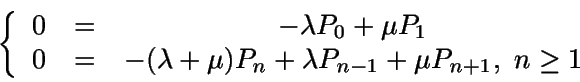
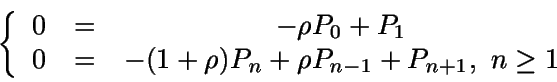
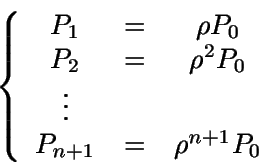
Así, como la suma de todas las probabilidades debe ser uno
y 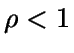 ,
se tiene
,
se tiene
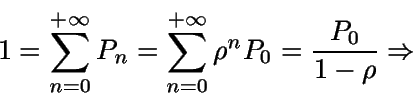
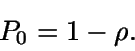
Luego
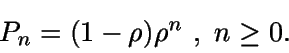
En consecuencia, la variable N (distribución estacionaria
del número de clientes en el sistema) sigue una distribución
geométrica 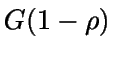 .
Se sigue que
.
Se sigue que
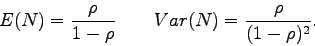
De igual modo, si por L se representa el número de clientes
en cola en el estdo estacionario, entonces
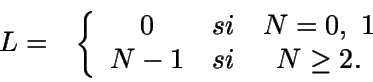
Las probabilidades asociadas son
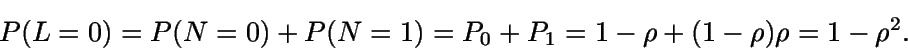
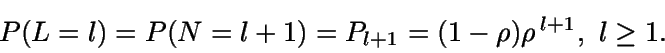
La esperanza de esta variable es
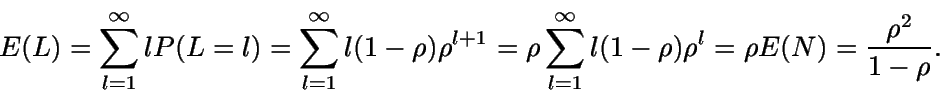
Finalmente, consideremos la variable V, tiempo de espera virtual
en estdo estacionario. Se trata de una variable mixta:
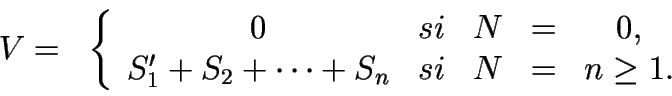
S'1 es el tiempo de servicio restante del cliente
que está en el servidor. Haciendo uso de la propiedad de pérdida
de memoria de la variable exponencial (pues 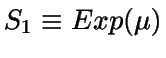 )
se tiene
)
se tiene
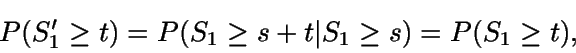
por lo que 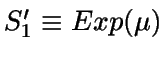 y es indistinto considerar la variable S1 o la variable
S'1 a efectos de calcular probabilidades.
y es indistinto considerar la variable S1 o la variable
S'1 a efectos de calcular probabilidades.
Ahora ya podemos calcular la función de distribución FV
asociada a la variable V.
Si v=0 entonces
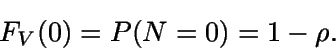
Si v>0, haciendo uso del teorema de la probabilidad compuesta (pues
el valor n asociado a v es aleatorio) y del hecho de que
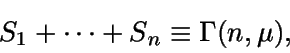
se tiene
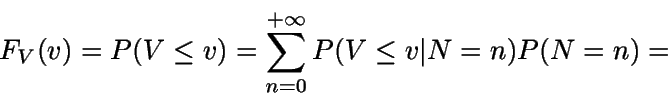
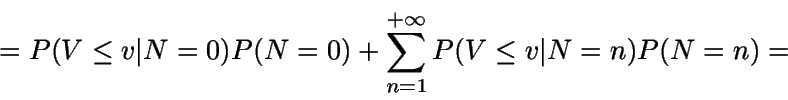
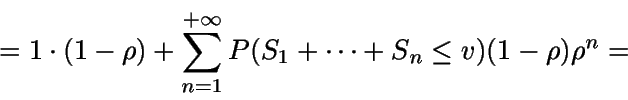

![\begin{displaymath}= (1-\rho) + (1-\rho)\lambda \int_0^v e^{-\mu t} e^{\lambda t......}{\lambda - \mu} \right] _0^v = 1 - \rho e^{(\lambda - \mu) v}.\end{displaymath}](img185.gif)
Luego
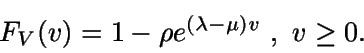
Análisis de los ciclos de ocupación y desocupación
Sea T0= la longitud de un ciclo de desocupación
y sea T1= la longitud de un ciclo de ocupación.
La longitud (media) de un ciclo de ocupación y desocupación
(en estado estacionario) será E(T0+T1).
Como, por la propiedad de pérdida de memoria, se tiene que 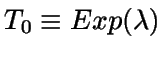 ,
entonces
,
entonces 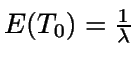 .
Por otra parte, como P0 representa la proporción
de tiempo que el servidor está desocupado (o lo que es lo mismo,
el sistema está vacío) en estado estacionario, entonces
.
Por otra parte, como P0 representa la proporción
de tiempo que el servidor está desocupado (o lo que es lo mismo,
el sistema está vacío) en estado estacionario, entonces
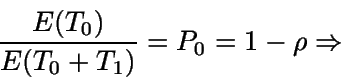
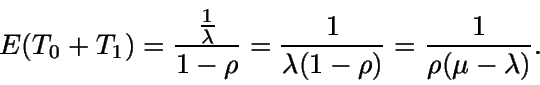
Diagrama de flujos para M/M/1
Definimos un grafo como sigue:
-
cada nodo representa un estado,
-
cada arco representa una transición entre estados,
-
en los arcos se indica la tasa de cambio.

Ahora vemos que se obtienen las mismas ecuaciones que se tenían
anteriormente, pues considerando que se produce una conservación
de flujos en el grafo se tiene:
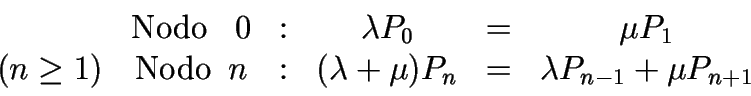
Interpretación: como  y
y 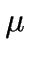 son, respectivamente, el número medio de llegadas y el de servicios
por unidad de tiempo, entonces
son, respectivamente, el número medio de llegadas y el de servicios
por unidad de tiempo, entonces 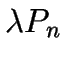 ,
,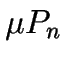 y
y 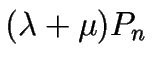 son a su vez el número de llegadas, el de servicios y el de sucesos
por unidad de tiempo en el estado n.
son a su vez el número de llegadas, el de servicios y el de sucesos
por unidad de tiempo en el estado n.
Control de una cola con un solo
servidor
Vamos a tratar de optimizar el funcionamiento de un sistema M/M/1 en el
que el servidor se ausenta a veces.
El servidor está atendiendo clientes hasta que el sistema se vacía.
Entonces él se retira y no vuelve a ofrecer su servicio hasta que
en la cola hay un número Q de clientes.
La tasa de llegadas es  y la de servicio es
y la de servicio es 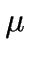 ,
siendo
,
siendo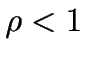 .
.
Se definen los siguientes costes del sistema:
-
coste de k unidades monetarias cada vez que el servidor vuelve (es
un coste fijo).
-
coste de h unidades monetarias por cada cliente en el sistema y
unidad de tiempo (coste de mantenimiento).
Se trata de determinar el valor de Q para que el sistema funciona
a coste mínimo por unidad de tiempo.
El coste de mantenimiento por unidad de tiempo (en promedio) es 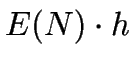 .
.
El coste fijo por unidad de tiempo es 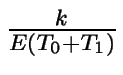 ,
pues E(T0+T1)
es la longitud media de un ciclo de ocupación y desocupación.
,
pues E(T0+T1)
es la longitud media de un ciclo de ocupación y desocupación.
Así, la función objetivo es
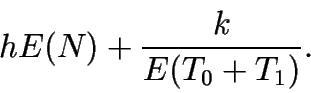
El diagrama de flujos asociado es el siguiente:
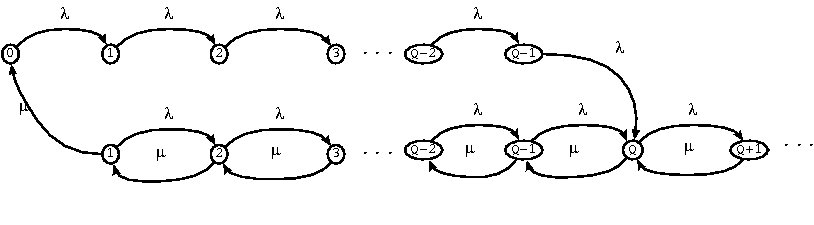
Además, para este problema se usa la siguiente notación:
-
Pn=P(N=n),
-
Pn(1)=P(N=n
y hay servidor),
-
Pn(0)=P(N=n
y no hay servidor).
Es inmediato que Pn=Pn(0)+Pn(1).
Se obtienen las siguientes ecuaciones:
(Nodos de arriba)
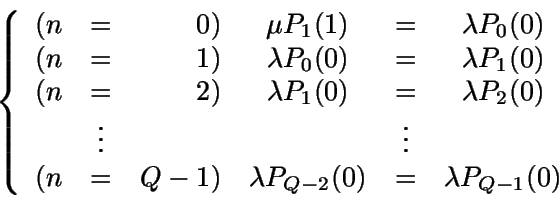
(Nodos de abajo)
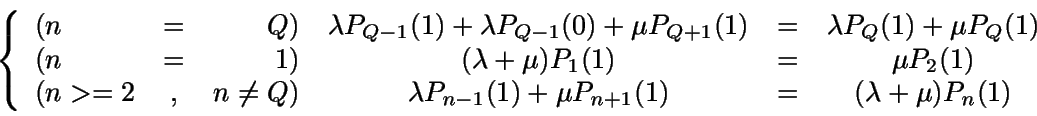
En definitiva:
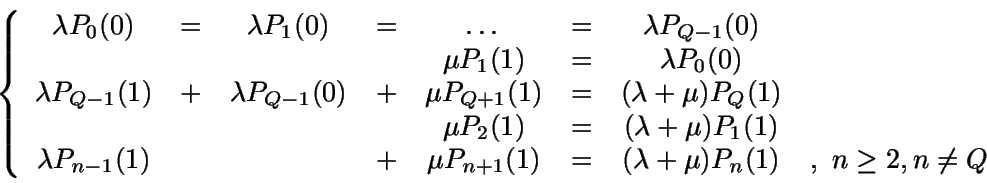
Para resolver este sistema vamos a utilizar la función generatriz
de probabilidades G(s) asociada a la variable aleatoria N.
Sea 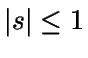 .
.
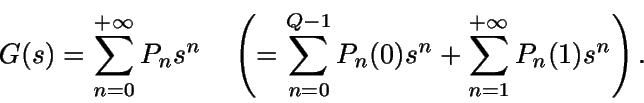
Si se define
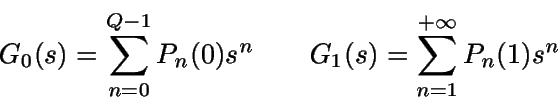
entonces
G(s)
= G0(s) + G1(s).
Como además
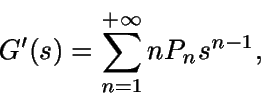
se tiene que
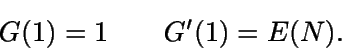
Si ahora se multiplica por sn+1 la
ecuación n-ésima en el sistema que se obtuvo:
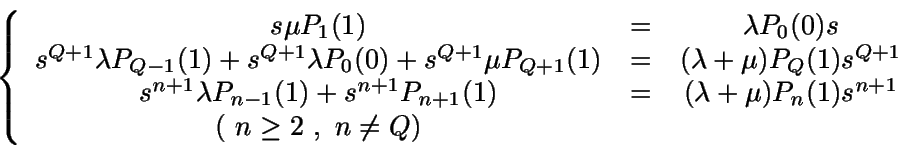
Sumando ahora todas estas igualdades:
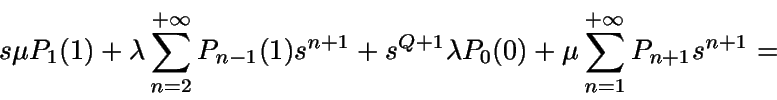
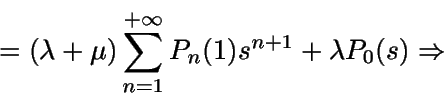
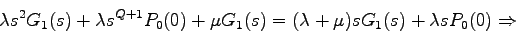
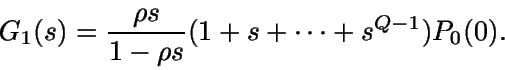
Por otra parte,
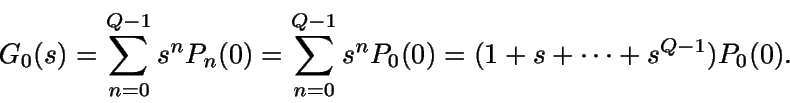
Así, evaluando G(s) en s=1 se tiene que
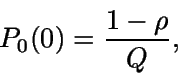
por lo que
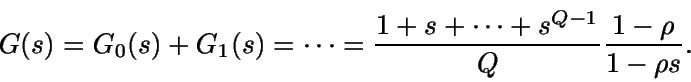
Ahora debemos calcular E(N) y E(T0+T1).
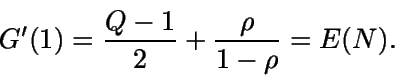
E(T0)= tiempo medio para que el sistema
pase de 0 a Q clientes.
Como el tiempo entre llegadas sigue una 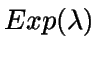 y esta distribución tiene pérdida de memoria, entonces es
equivalente a calcular Q veces el tiempo medio para que llegue un cliente.
y esta distribución tiene pérdida de memoria, entonces es
equivalente a calcular Q veces el tiempo medio para que llegue un cliente.
![\begin{displaymath}E(T_0) = Q E[Exp(\lambda)] = Q \ \frac {1}{\lambda} = \frac{Q}{\lambda}.\end{displaymath}](img209.gif)
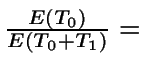 probabilidad de que haya 0,1,..., Q-1 clientes en el sistema en estado
estacionario y no haya servidor
probabilidad de que haya 0,1,..., Q-1 clientes en el sistema en estado
estacionario y no haya servidor
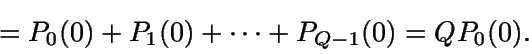
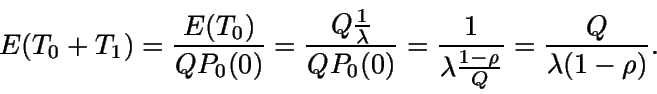
Así
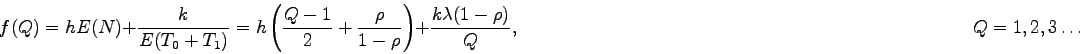
Buscamos el valor donde f alcance su mínimo; si Q tomara
valores reales,
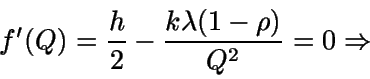
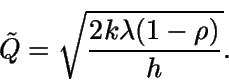
Como
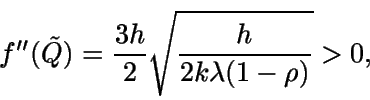
entonces 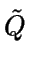 sería mínimo local y global.
sería mínimo local y global.
Como Q sólo toma valores naturales y la función f es convexa,
entonces la solución óptima Q* será
la que dé el mínimo de entre f([Q*])
y f([Q*]+1).
El valor
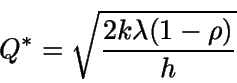
se denomina tamaño de lote de Wilson.

![]() .
Recíprocamente, se tiene el siguiente resultado:
.
Recíprocamente, se tiene el siguiente resultado:
![]() son independientes, siendo Ti el tiempo transcurrido
entre las llegadas (i-1)-ésima e i-ésima, todas ellas con
distribución
son independientes, siendo Ti el tiempo transcurrido
entre las llegadas (i-1)-ésima e i-ésima, todas ellas con
distribución ![]() ,
entonces
,
entonces ![]() .
.
![]() .
.