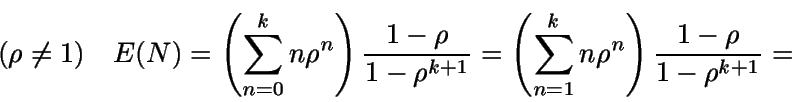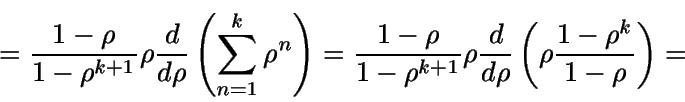Siguiente:Comportamiento
transitorio de M/M/1/1Nivel anterior:Modelos
de colas estocásticosPrevia:El
modelo M/M/1
El sistema M/M/1/k
Diagrama de flujo en estado estacionario :
 Ecuaciones de equilibrio:
Ecuaciones de equilibrio:
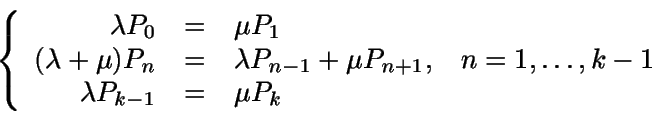
Su solución es 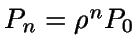 ,
n=0,1,..., k.
,
n=0,1,..., k.
En estado estacionario se tendrá
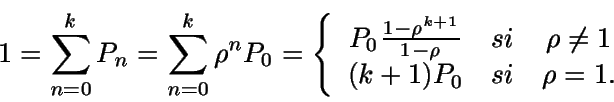
Así
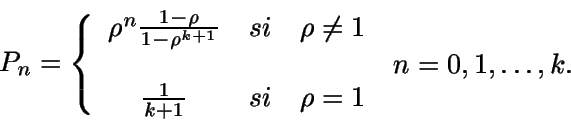
Distribución del número de clientes en cola (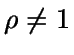 )
)
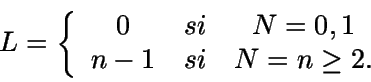
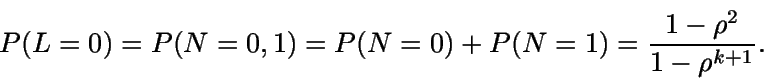
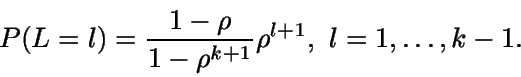
Número medio de clientes en el sistema
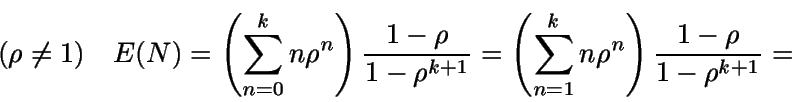
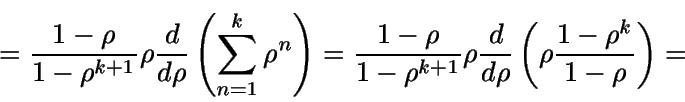
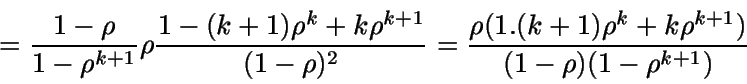



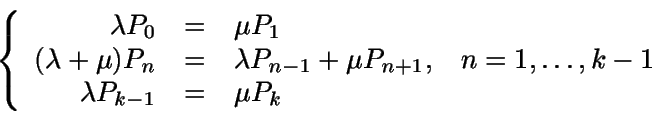
![]() ,
n=0,1,..., k.
,
n=0,1,..., k.
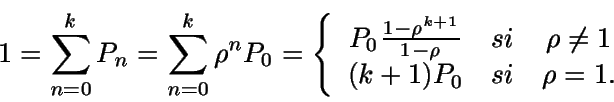
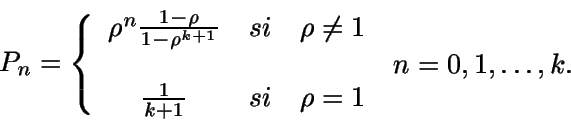
![]() )
)