Caso práctico resuelto
Introducción
A veces se dispone de un conjunto de observaciones y se pretende ordenarlas en grupos de manera que el grado de asociación entre los miembros del mismo grupo sea alto y bajo entre miembros de grupos diferentes. Por ejemplo, podríamos estar interesados en agrupar Comunidades Autónomas por similitud en diversas variables socioeconómicas. En este contexto, una técnica adecuada es el análisis de conglomerados.
Datos del problema
El Instituto Nacional de Estadística (http://www.ine.es) proporciona información a nivel autonómico de numerosas variables socioeconómicas. Entre ellas, y para el año 2014, podemos encontrar:
- tasainm: tasa bruta de inmigración (personas/mil habitantes)
- tasaem: tasa bruta de emigración (personas/mil habitantes)
- tasaact: tasa actividad (activos/p.total)
- tasaempleo: tasa de empleo (ocupados/p.total)
- tasaparo: tasa de paro (parados/activos)
- ipc: IPC base 2016
- pibpc: PIB a precios corrientes por individuo
Con esta información vamos a agrupar las comunidades autónomas, incluyendo las ciudades autónomas de Ceuta y Melilla, con una situación similar. En concreto, queremos identificar grupos de comunidades autónomas (conglomerados) que tengan un comportamiento similar en los indicadores anteriores. Estos indicadores a nivel autonómico se encuentran en el objeto ccaa del fichero conglomerados.RData. Además, este fichero incluye estas mismas variables a nivel provincial (prov) y dos objetos de naturaleza espacial (ccaasf y provsf) que se emplearán para representar los conglomerados en mapas, tanto a nivel de comunidad autónoma como a nivel provincial.
Etapa 1. Exploración de los datos
En primer lugar, hay que cargar los datos (guarde el fichero en el directorio de trabajo)
load("conglomerados.RData")y realizar una visualización preliminar del objeto con los datos de interés (ccaa),
summary(ccaa)## tasainm tasaem tasaact tasaemp
## Min. : 4.663 Min. : 5.084 Min. :51.63 Min. :38.87
## 1st Qu.: 7.317 1st Qu.: 7.051 1st Qu.:55.91 1st Qu.:41.53
## Median : 8.901 Median : 9.003 Median :58.96 Median :44.43
## Mean :10.267 Mean :10.733 Mean :58.61 Mean :45.01
## 3rd Qu.:11.663 3rd Qu.:11.286 3rd Qu.:60.95 3rd Qu.:48.60
## Max. :27.724 Max. :26.380 Max. :64.82 Max. :53.15
## tasaparo ipc pibpc
## Min. :14.92 Min. :100.1 Min. :15224
## 1st Qu.:18.54 1st Qu.:100.7 1st Qu.:18218
## Median :20.78 Median :100.8 Median :19664
## Mean :23.21 Mean :100.8 Mean :21479
## 3rd Qu.:29.01 3rd Qu.:101.0 3rd Qu.:24478
## Max. :34.23 Max. :101.5 Max. :30638Es fácil observar que las variables no tienen el mismo recorrido o rango (por ejemplo, pibpc y tasainm), por lo que sería conveniente, para que todas pesen lo mismo en el análisis, trabajar con los datos tipificados, ya que las medidas de disimilaridad son muy sensibles a las unidades de medida.
ccaa_tip <- scale(ccaa) # Obtención de la matriz de datos tipificadaEtapa 2. Detección de valores atípicos
Con objeto de detectar los posibles valores atípicos se pueden representar gráficamente las variables utilizando un diagrama de cajas (en este caso, de los datos tipificados). El diagrama es sencillo de realizar, y puede completarse, con un poco de programación adicional, incorporando etiquetas a los valores atípicos en caso de que existan.
par(cex.axis=0.8)
bx1 <- boxplot(ccaa_tip, col = "lightyellow")
# OPCIONAL: utlizar lo siguiente solo si quiere colocar etiquetas a los valores atípicos o extremos
if(length(bx1$out)!= 0){
out.rows <- sapply(1:length(bx1$out), function(i)
which(ccaa_tip[ ,bx1$group[i]] == bx1$out[i]))
text(bx1$group, bx1$out, rownames(ccaa_tip)[out.rows], pos=4, cex = 0.8)
}
Este gráfico nos muestra que Ceuta y Melilla presentan valores atípicos en las tasas de emigración e inmigración, mientras que Cataluña es en el IPC. No obstante, optamos por conservar todas las Comunidades Autónomas, incluidas las Ciudades Autónomas de Ceuta y Melilla aunque, posiblemente, su comportamiento diferencial las agrupe en el análisis.
Etapa 3. Estudio de la correlación
Para medir el grado de relación entre cada dos variables cuantitativas, calculamos la matriz de correlaciones aplicando la función cor sobre los datos (da igual hacerlo sobre los datos originales o sobre los tipificados, ya que la correlación es independiente de la escala de medida de las variables). Recordemos que una correlación cercana a 1 o -1 indica que existe una fuerte relación lineal entre las variables, en el primer caso directa y en el segundo inversa, mientras que valores cercanos a cero indicarían ausencia de relación lineal.
cor(ccaa_tip)## tasainm tasaem tasaact tasaemp tasaparo
## tasainm 1.00000000 0.932739282 0.130991883 -0.1142625 0.252836019
## tasaem 0.93273928 1.000000000 -0.007655524 -0.3081243 0.385751985
## tasaact 0.13099188 -0.007655524 1.000000000 0.5930565 0.007151169
## tasaemp -0.11426250 -0.308124338 0.593056488 1.0000000 -0.800302466
## tasaparo 0.25283602 0.385751985 0.007151169 -0.8003025 1.000000000
## ipc -0.07284412 0.165152899 -0.387430150 -0.4985037 0.324407500
## pibpc -0.15829974 -0.333594290 0.424970550 0.9059509 -0.809466927
## ipc pibpc
## tasainm -0.07284412 -0.1582997
## tasaem 0.16515290 -0.3335943
## tasaact -0.38743015 0.4249705
## tasaemp -0.49850373 0.9059509
## tasaparo 0.32440750 -0.8094669
## ipc 1.00000000 -0.5476956
## pibpc -0.54769563 1.0000000Observe que resulta mucho más sencillo interpretar estas matrices si no se utiliza un número de decimales tan elevado. Una manera de reducirlo es utilizando la función round, de forma que en adelante la emplearemos con dicho objetivo:
round(cor(ccaa_tip), 2)## tasainm tasaem tasaact tasaemp tasaparo ipc pibpc
## tasainm 1.00 0.93 0.13 -0.11 0.25 -0.07 -0.16
## tasaem 0.93 1.00 -0.01 -0.31 0.39 0.17 -0.33
## tasaact 0.13 -0.01 1.00 0.59 0.01 -0.39 0.42
## tasaemp -0.11 -0.31 0.59 1.00 -0.80 -0.50 0.91
## tasaparo 0.25 0.39 0.01 -0.80 1.00 0.32 -0.81
## ipc -0.07 0.17 -0.39 -0.50 0.32 1.00 -0.55
## pibpc -0.16 -0.33 0.42 0.91 -0.81 -0.55 1.00Esta matriz también se puede representar gráficamente,
library(corrplot)
corrplot.mixed(cor(ccaa_tip))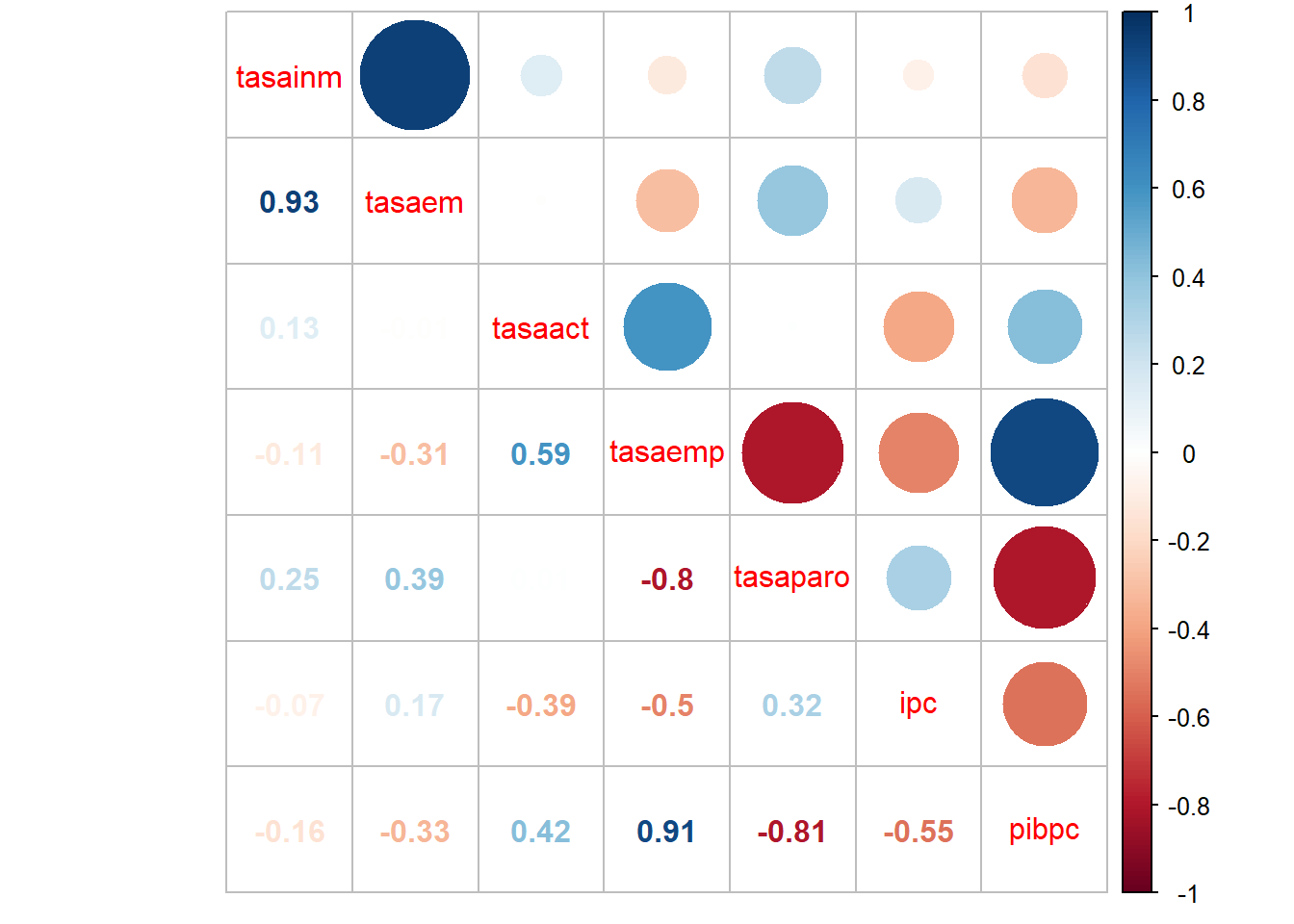
Observando la matriz de correlaciones o el gráfico anterior podemos ver que existen algunas correlaciones grandes entre las variables (por ejemplo, entre la tasa de emigración y la tasa de inmigración, o entre el PIBpc y la tasa de empleo). La cuestión es si estas correlaciones son lo suficientemente grandes para influir en la matriz de distancias cuando se utiliza la distancia euclídea.
Si consideramos que las correlaciones son suficientemente grandes para influir en la matriz de distancias sería conveniente realizar un análisis de componentes principales primero y realizar el análisis de conglomerados a partir de los resultados de este, ya que las componentes obtenidas serían incorreladas. Si pensamos que las correlaciones no son suficientemente grandes podemos realizar el análisis sobre las variables originales.
Comenzaremos suponiendo que las correlaciones no son suficientemente grandes, y lo repetiremos suponiendo que sí, para observar si las correlaciones entre las variables afectan a la formación y composición de conglomerados.
Etapa 4. Selección de la medida de similitud y la técnica de agrupación
En primer lugar, debe elegirse la medida de distancia a emplear para decidir qué comunidades autónomas son las más parecidas y cuáles presentan mayores diferencias según las variables de interés. Entre las medidas de distancia que se pueden emplear para variables métricas, como las disponibles en este caso, se encuentran la distancia euclídea, la distancia euclídea al cuadrado, la distancia de Minkowski y la distancia city block o “Manhattan”. Cualquiera de estas distancias se puede calcular utilizando la función dist mediante el argumento method.
Si suponemos, inicialmente, que las correlaciones entre las variables de interés no son suficientemente elevadas como para realizar un análisis de componentes principales previo, procederemos utilizando la distancia euclídea aplicada sobre la matriz de datos tipificados. Esta distancia es la que se emplea con más frecuencia y está implementada por defecto en la función dist.
distancia <- dist(ccaa_tip)
round(as.matrix(distancia)[1:19,1:6], 2) # visualización de parte de la matriz de distancias## Andalucía Aragón Asturias Baleares Canarias Cantabria
## Andalucía 0.00 3.83 3.27 4.84 1.58 3.66
## Aragón 3.83 0.00 2.93 2.84 2.85 1.43
## Asturias 3.27 2.93 0.00 4.76 3.48 2.29
## Baleares 4.84 2.84 4.76 0.00 4.05 3.86
## Canarias 1.58 2.85 3.48 4.05 0.00 2.83
## Cantabria 3.66 1.43 2.29 3.86 2.83 0.00
## Castilla-León 3.52 1.91 2.03 4.43 2.85 0.75
## Castilla-La Mancha 3.25 3.25 3.70 4.82 2.37 2.55
## Cataluña 4.51 2.92 4.50 2.22 4.03 4.12
## ComValenciana 2.39 1.59 2.40 3.19 1.68 1.69
## Extremadura 1.89 3.54 2.40 5.20 2.15 2.73
## Galicia 3.07 2.46 1.07 4.72 2.97 1.71
## Madrid 5.51 2.65 5.40 2.32 4.37 4.01
## Murcia 1.97 2.28 3.12 3.18 1.04 2.40
## Navarra 4.89 1.56 3.87 2.22 4.04 2.85
## País Vasco 4.76 2.40 3.61 2.77 4.33 3.51
## Rioja 4.29 1.09 3.36 2.03 3.37 2.07
## Ceuta 4.35 4.58 5.12 4.64 3.83 4.46
## Melilla 5.40 5.50 5.28 5.37 5.22 5.19Esta matriz de distancias nos muestra, por ejemplo, que Cataluña y Melilla son las regiones más disimilares (con una distancia de 6.84), mientras que Cantabria y Castilla-León son las más similares (con una distancia de 0.75).
Una vez obtenida la matriz de disimilaridades, la siguiente etapa es decidir el método de agrupación a utilizar. Vamos a comenzar planteando un análisis de conglomerados jerárquico, para luego realizar un análisis no jeráquico de k-medias.
Conglomerado Jerárquico con hclust
En un método jeráquico es preciso establecer el método de agrupación de los elementos, en nuestro caso, las regiones autónomas. Existen varios métodos disponibles, como el vecino más cercano o enlace simple (single), el vecino más lejano o enlace completo (complete), agrupación de centroides o enlace centroide (centroid), enlace promedio ponderado entre grupos (average), y sin ponderar (mcquitty), y enlace de mínima varianza o método de Ward (ward.D o ward.D2). Todos estos métodos se pueden implementar dentro de la función hclust cambiando el argumento method.
A continuación, vamos a calcular los grupos utilizando tres métodos, complete (el que tiene predeterminado la función hclust), average (que viene por defecto en otros paquetes estadísticos como SPSS) y ward.D2 (que suele ser el método que mejor clasifica).
Método complete
Creamos un objeto de R que contenga la información que ofrece la función hclust y sobre el cual se puede dibujar:
clust <- hclust(distancia, method = "complete") # Como el método por defecto es el `complete` no sería necesario especificarlo
plot(clust, hang = -1) # Con el argumento hang=-1, conseguimos que las etiquetas aparezcan alineadas por debajo de 0 en el eje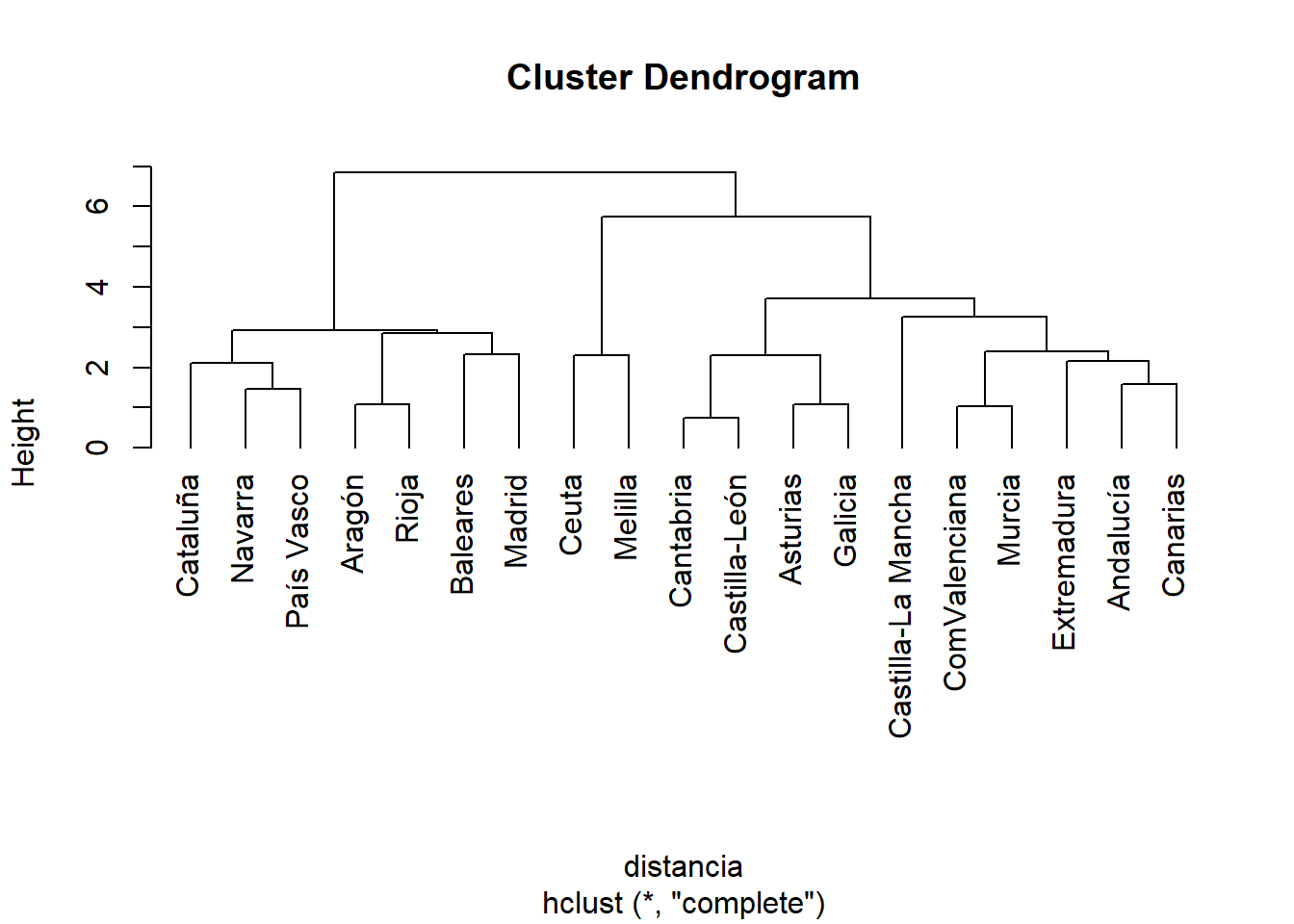
Si se decidiese cortar en el dendograma por una altura de seis en el eje de ordenadas, saldrían dos grupos, uno formado por Cataluña, Navarra, País Vasco, Aragón, La Rioja, Baleares y Madrid, y otro formado por el resto de las comunidades autónomas junto a Ceuta y Melilla.
plot(clust, hang = -1)
abline(h=6, col="red")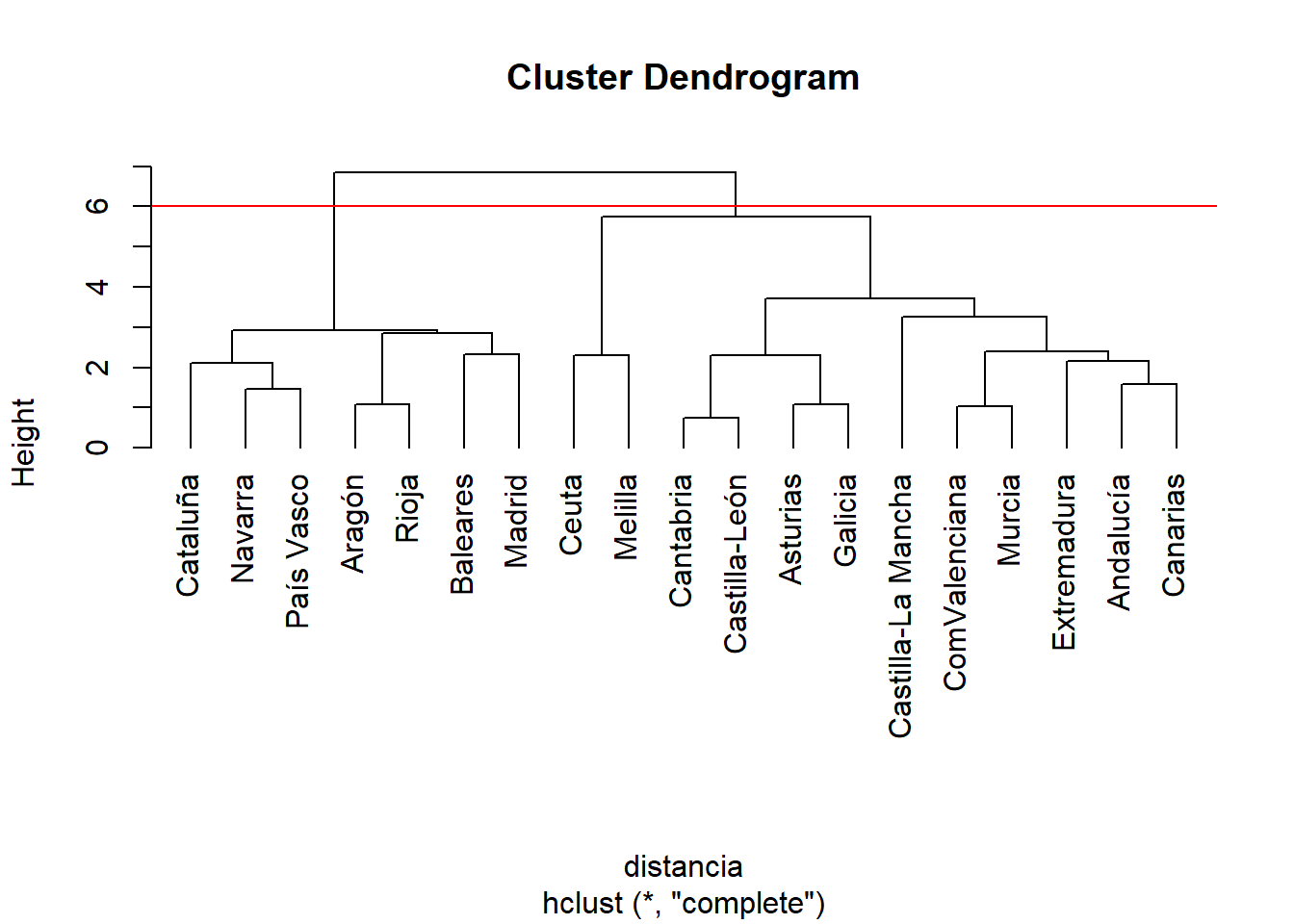
Si el corte se hiciera en otro punto distinto, el número de grupos podría ser diferente, por ejemplo:
par(mfrow=c(1,2))
plot(clust, hang = -1)
abline(h=4, col="red")
plot(clust, hang = -1)
abline(h=2.5, col="red")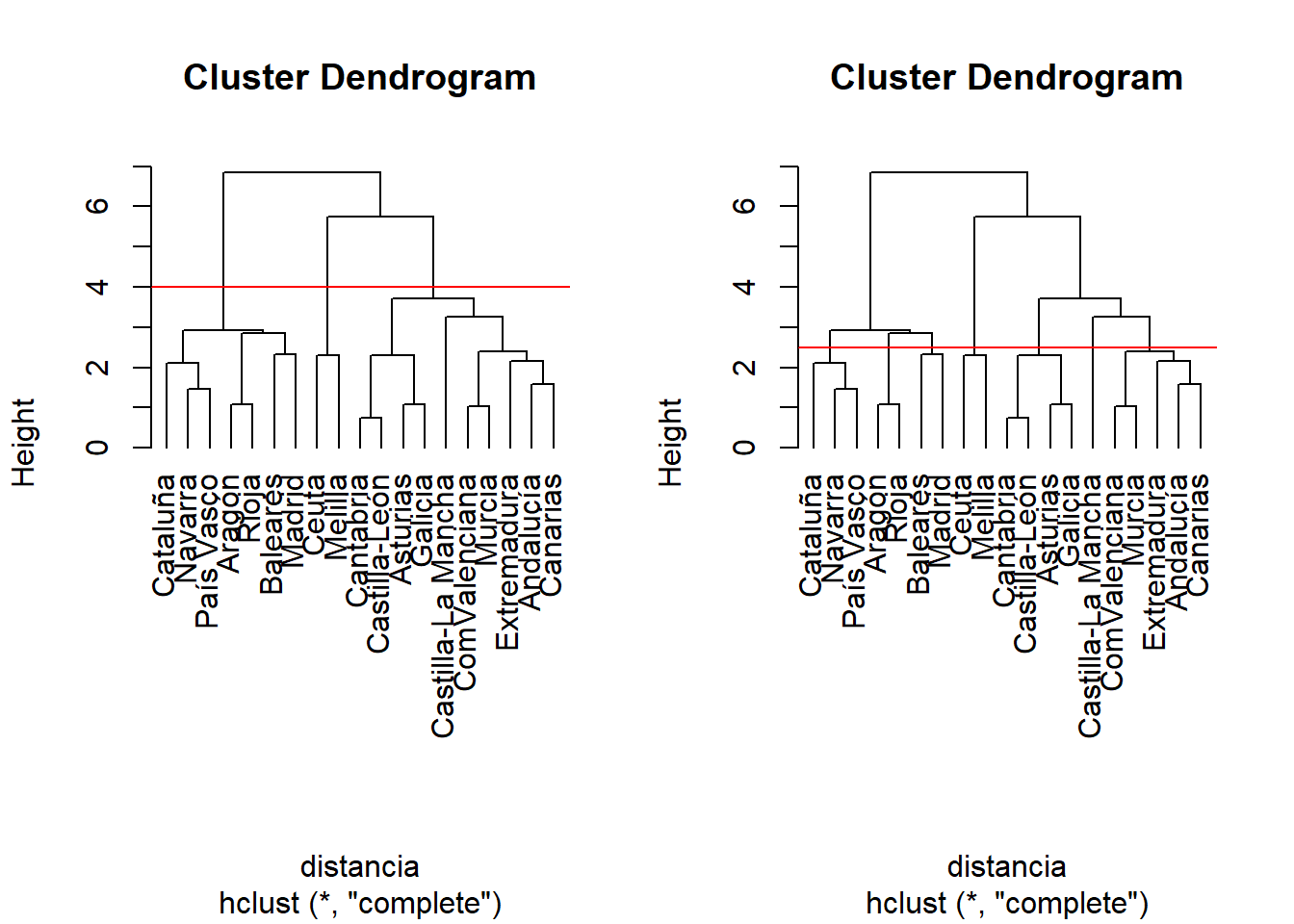
¿Cómo saber cuál es la agrupación adecuada? Hay que elegir aquella que tenga sentido en el contexto que se está analizando, aunque podemos apoyarnos en algunas funciones que tiene R implementadas para este fin. La función NbClust del paquete NbClust sirve para este próposito, calculando el número de conglomerados a partir de varios índices:
library(NbClust) # Determinar número de conglomerados
numero.conglomerado.complete <- NbClust(ccaa_tip, distance = "euclidean", min.nc = 2, max.nc = 11, method = "complete", index ="all")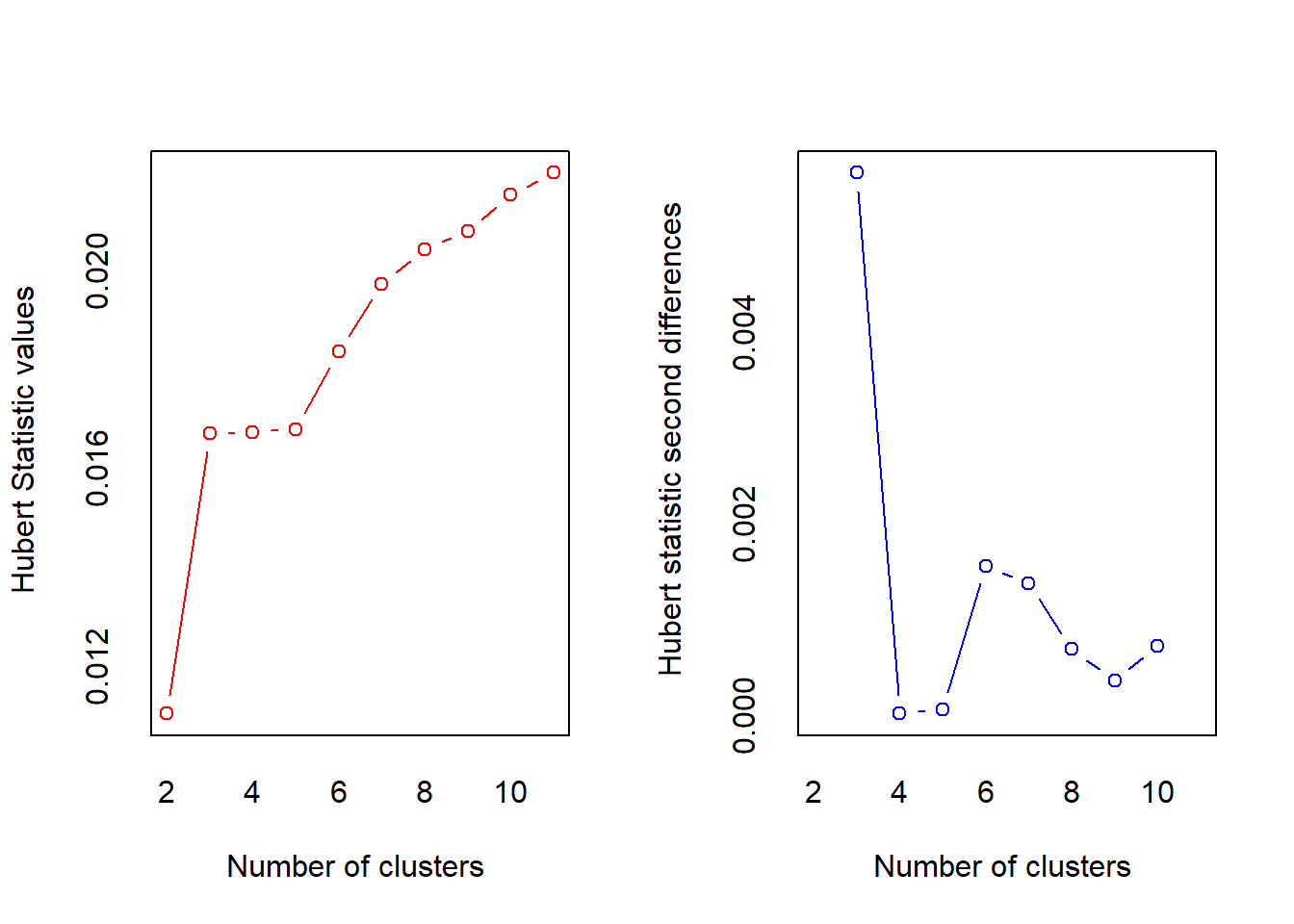
## *** : The Hubert index is a graphical method of determining the number of clusters.
## In the plot of Hubert index, we seek a significant knee that corresponds to a
## significant increase of the value of the measure i.e the significant peak in Hubert
## index second differences plot.
## 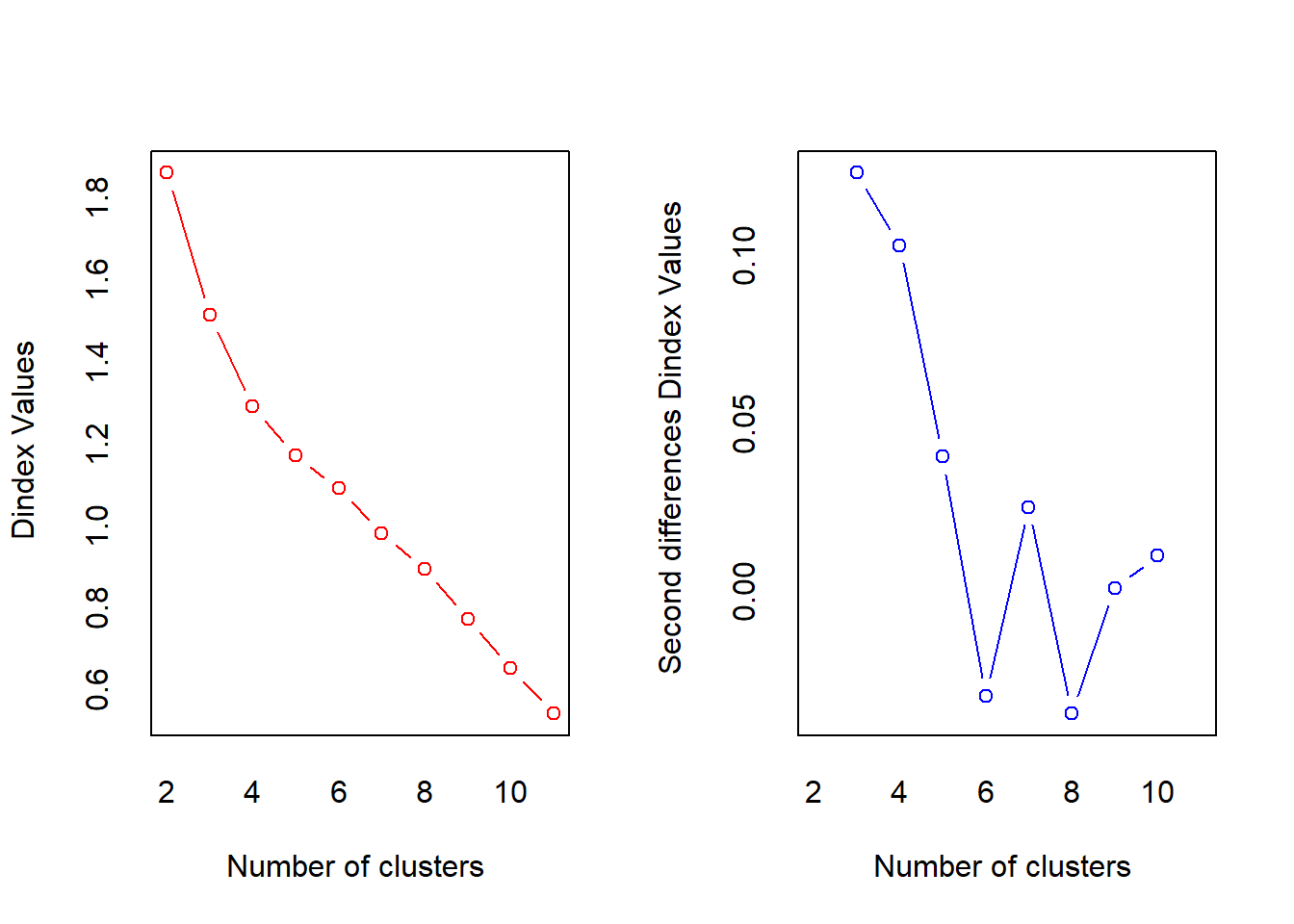
## *** : The D index is a graphical method of determining the number of clusters.
## In the plot of D index, we seek a significant knee (the significant peak in Dindex
## second differences plot) that corresponds to a significant increase of the value of
## the measure.
##
## *******************************************************************
## * Among all indices:
## * 4 proposed 2 as the best number of clusters
## * 9 proposed 3 as the best number of clusters
## * 4 proposed 4 as the best number of clusters
## * 1 proposed 7 as the best number of clusters
## * 2 proposed 10 as the best number of clusters
## * 3 proposed 11 as the best number of clusters
##
## ***** Conclusion *****
##
## * According to the majority rule, the best number of clusters is 3
##
##
## *******************************************************************En la salida de esta función se muestra información sobre dos de los índices, Hubert y D-index. Para cada índice se ofrecen dos gráficos: el propio índice (en rojo), y las diferencias de los índices para números de conglomerados consecutivos (en azul). El número de conglomerados a seleccionar será aquel que presente una mayor diferencia (valor más alto en el gráfico azul). Según este criterio ambos índices nos indican que el número de conglomerados adecuado sería tres.
Además, esta salida también proporciona una tabla resumen con los resultados de los diferentes índices que calcula, así como una conclusión sobre el mejor número de conglomerados a utilizar.
Una vez decidido el número de conglomerados (3, en este caso), éstos se obtienen con la función cutree aplicada sobre el objeto clust obtenido con hclust.
sol <- cutree(clust, k = 3)
sol## Andalucía Aragón Asturias
## 1 2 1
## Baleares Canarias Cantabria
## 2 1 1
## Castilla-León Castilla-La Mancha Cataluña
## 1 1 2
## ComValenciana Extremadura Galicia
## 1 1 1
## Madrid Murcia Navarra
## 2 1 2
## País Vasco Rioja Ceuta
## 2 2 3
## Melilla
## 3Otra forma de presentar esta información es por conglomerado,
sort(sol)## Andalucía Asturias Canarias
## 1 1 1
## Cantabria Castilla-León Castilla-La Mancha
## 1 1 1
## ComValenciana Extremadura Galicia
## 1 1 1
## Murcia Aragón Baleares
## 1 2 2
## Cataluña Madrid Navarra
## 2 2 2
## País Vasco Rioja Ceuta
## 2 2 3
## Melilla
## 3La solución de la función cutree junto con los datos originales ccaa los almacenaremos en un objeto al que llamamos resccaa para su posterior análisis.
resccaa <- ccaa
resccaa$conglomerado <- solSi nos fijamos en la salida de la función cutree se puede ver como el primer grupo estaría formado por Andalucía, Asturias, Canarias, Cantabria, Castilla-León, Castilla-La Mancha, Comunidad Valenciana, Extremadura, Galicia y Murcia. El segundo conglomerado agruparía a Aragón, Islas Baleares, Cataluña, Madrid, Navarra, País Vasco y la Rioja, y el último grupo estaría formado por las ciudades autónomas de Ceuta y Melilla, como era de esperar al presentar estas dos ciudades valores atípicos en las tasas de emigración e inmigración. Obsérvese que el primer grupo es el más numeroso, con 10 de las 17 comunidades autónomas. Dentro de este grupo podrían apreciarse dos subgrupos, uno con comunidades del norte (Asturias, Cantabria, Castilla-León y Galicia), y otro con las comunidades del sur más las Islas Canarias (Andalucía, Canarias, Castilla-La Mancha, Comunidad Valenciana, Extremadura y Murcia).
Una manera de visualizar el resultado del análisis de conglomerados es con la función fviz_cluster del paquete factoextra,
library(factoextra)
fviz_cluster(hcut(ccaa_tip, k = 3, hc_method = "complete"), palette = "rainbow_hcl")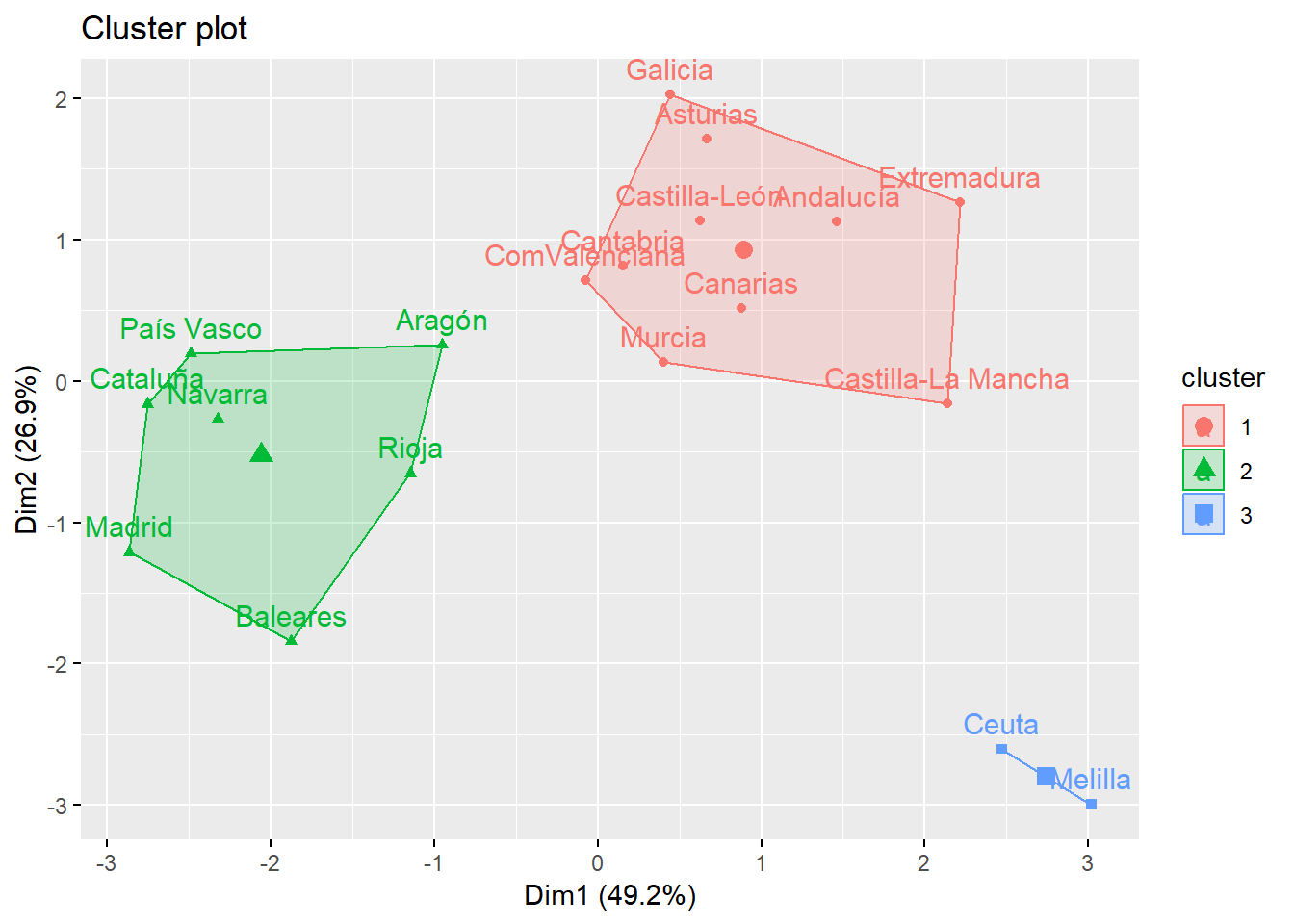
También se podría utilizar un mapa de España para representar los conglomerados, ya que los individuos que se desean agrupar son las comunidades autónomas,
library(colorspace) # color mapas
library(rgdal) # mapask <- 3 # número de conglomerados
resccaa$COM = c("CA01","CA02","CA03","CA04","CA05","CA06","CA07","CA08","CA09","CA10","CA11","CA12","CA13","CA14","CA15","CA16","CA17","CA18","CA19")
ccaasfC <- merge(ccaasf, resccaa, by = "COM")
colores <- rainbow_hcl(k)
color<- as.character(factor(ccaasfC$conglomerado, labels = colores))
plot(ccaasfC, col = color)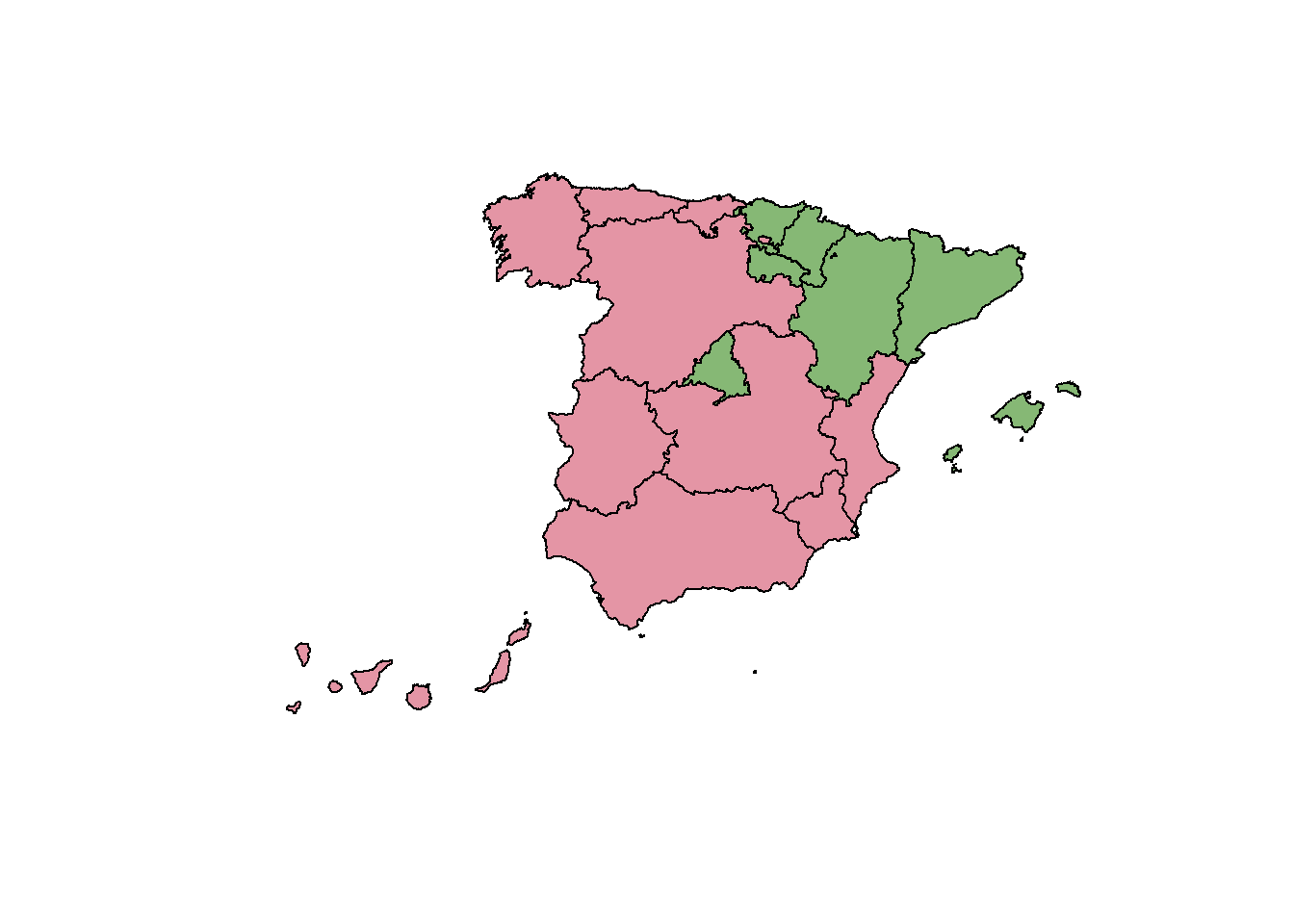
Método average
Si repetimos el análisis anterior pero con el método average, podemos ver que el número de grupos más adecuado también es 3 (ver el dendograma y la función NbClust) y que, además, cada grupo contiene los mismos elementos que con el método complete (omitimos la salida de R por ser similar, aunque incluimos el código).
# Análisis de conglomerados con el método de ward
clust <- hclust(distancia, method = "average")
# Obtención del dendograma
plot(clust, hang = -1)
# Determinación del número de conglomerados
numero.conglomerado.average <- NbClust(ccaa_tip, distance = "euclidean", min.nc = 2,
max.nc = 10, method = "average", index ="all")
# Solución obtenida
sol2 <- cutree(clust, k = 3)
# Comparación con la solución obtenida con el método complete
table(sol, sol2)
Método ward.D2
si repite de nuevo todo lo anterior utilizando el método ward.D2 observará que la agrupación obtenida es similar.
# Análisis de conglomerados con el método de ward
clust <- hclust(distancia, method = "ward.D2")
# Obtención del dendograma
plot(clust, hang = -1)
# Determinación del número de conglomerados
numero.conglomerado.ward <- NbClust(ccaa_tip, distance = "euclidean", min.nc = 2,
max.nc = 10, method = "ward.D2", index ="all")
# Solución obtenida
sol3 <- cutree(clust, k = 3)
# Comparación con la solución obtenida con los otros dos métodos
table(sol, sol2, sol3)
Matriz cofenética
Una forma de comparar los resultados de los distintos métodos jerárquicos es la obtención del coeficiente de correlación entre la matriz de distancias original y la matriz cofenética de la agrupación resultante de un método jerárquico concreto.
A continuación calculamos, a modo de ejemplo, la matriz cofenética para los resultados obtenidos con el método complete y el coeficiente de correlación entre los datos de esta matriz y los de la matriz de distancias original.
# para el método "complete"
matcof <- cophenetic(hclust(distancia, method = "complete")) # matriz cofenética
cor(distancia, matcof) # coeficiente de correlación## [1] 0.7003826Como lo deseable es calcular los coeficientes de correlación para cada uno de los métodos disponibles en la función hclust, con objeto de compararlos, puede repetir el cálculo y obtendrá los siguientes resultados,
## Método Coef. correl. cofenético
## 1 single 0.67
## 2 complete 0.7
## 3 centroid 0.67
## 4 average 0.81
## 5 mcquitty 0.79
## 6 ward.D 0.65
## 7 ward.D2 0.69Puede observarse que el mayor coeficiente de correlación corresponde al método average siendo por tanto, el que mejor representa la estructura original de distancias en la nueva agrupación en conglomerados que propone.
Por último, puede comprobarse que, de haber trabajado con los resultados de un análisis de componentes principales previo, el número de conglomerados más adecuado y su composición habrían sido los mismos, por lo que parece que las correlaciones no están jugando un papel importante en la obtención de estos grupos.
plot(hclust(dist(prcomp(ccaa_tip)$x), method = "average"), hang = -1)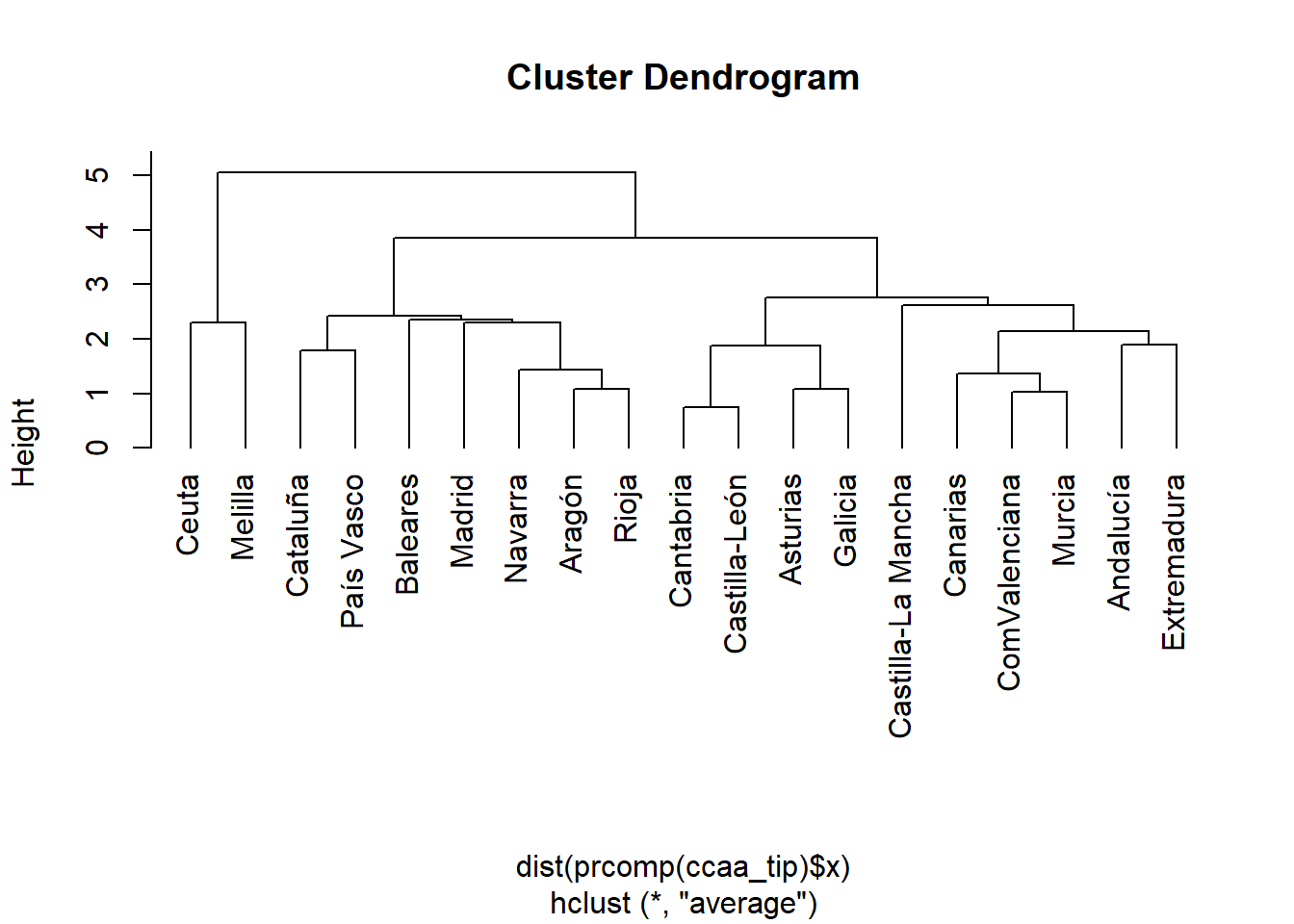
Conglomerado no Jerárquico con kmeans
Este método consiste en clasificar a los individuos en un número \(k\) de grupos fijado de antemano. Cada grupo viene representado por el vector de medias de las variables para los individuos que pertenecen a él, denominado centroide.
Una vez fijado \(k\), el algoritmo del método kmeans comienza asignando, de forma arbitaria, una observación a cada uno de los conglomerados. Esta asignación constituye el centroide inicial. Las observaciones restantes se van incorporando al grupo más cercano (en términos de distancia euclídea entre la observación y el centroide del grupo). Tras esta asignación, el algoritmo calcula de nuevo el centroide para cada conglomerado y reasigna las observaciones con el criterio de que estén incluidas en el conglomerado más cercano. Los centroides se van recalculando y el proceso se repite hasta que los conglomerados cambian poco entre etapas, o bien se llega al número máximo de iteraciones fijado a priori (número arbitrario).
Los principales problemas de este tipo de análisis son la determinación del número \(k\) de grupos y la selección de los \(k\) centros iniciales (ya que los resultados son sensibles a los puntos utilizados como inicio, a los denominados puntos semilla). Existen varias herramientas que nos ayudan a solventar en parte estas cuestiones:
- Determinación del número \(k\) de grupos. Se puede utilizar el gráfico de sedimentación o un método de conglomerados jerárquico. El gráfico de sedimentación es la representación gráfica de la variabilidad dentro de los grupos para cada valor de \(k\), siendo \(k\) el número de grupos. Esta variabilidad desciende con el número de grupos, por lo que el \(k\) elegido será aquel en el que esta reducción se estabiliza (se observa un codo). El gráfico se obtiene con la función
fviz_nbclustdel paquetefactoextracon la opciónwssen el argumentomethod.
fviz_nbclust(ccaa_tip, kmeans, method = "wss") 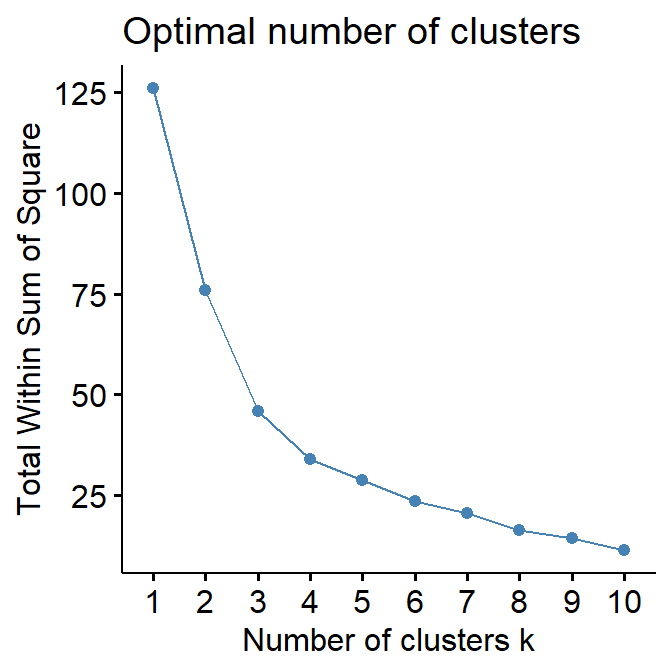
El gráfico de sedimentación indica que el número de conglomerados a considerar podría ser 3 o 4, mientras que en el análisis jerárquico habíamos determinado la existencia de 3 grupos, uno con 2 subgrupos. Ambos resultados son compatibles.
- Selección de los \(k\) centros iniciales. Se pueden considerar como centros de inicio los centroides de los grupos determinados en el análisis jerárquico, o repetir el algoritmo kmedias con distintos centros iniciales hasta encontrar una partición estable. La utilización de más de un conjunto de centros de inicio, reduce la dependencia de la partición de los puntos semilla.
La función kmeans permite considerar uno o varios conjuntos de centros de inicio fijados aleatoriamente, a través de su argumento nstart y establecer el número de grupos o quienes son los centroides iniciales con centers. Así, si se desea agrupar los individuos en \(k\) grupos (centers = k) con un único conjunto de centros de inicio aleatorios se utilizará nstart = 1 o con más de uno (nstart > 1), mientras que para utilizar los centroides obtenidos en un análisis jerárquico habrá que sustituir en el argumento centers el valor de k por el nombre del objeto que contiene a dichos centroides.
a) kmeans con el número de grupos fijado a priori y con varios centros de inicio aleatorios.
El número de grupos considerados es tres y se fuerza al algoritmo a elegir 100 conjuntos de centros de inicio aleatorios. El algoritmo determina como solución aquella agrupación que minimiza la variabilidad dentro de los conglomerados.
km1 <- kmeans(ccaa_tip, centers = 3, nstart = 100)
km1## K-means clustering with 3 clusters of sizes 2, 10, 7
##
## Cluster means:
## tasainm tasaem tasaact tasaemp tasaparo ipc
## 1 2.42341846 2.5199234 -0.1103369 -1.0813154 1.2771953 -0.1368348
## 2 -0.45375230 -0.3051431 -0.4315810 -0.5666043 0.3739426 0.6001862
## 3 -0.04418771 -0.2840594 0.6480692 1.1183820 -0.8991167 -0.8183132
## pibpc
## 1 -0.8660104
## 2 -0.6229819
## 3 1.1374057
##
## Clustering vector:
## Andalucía Aragón Asturias
## 2 3 2
## Baleares Canarias Cantabria
## 3 2 2
## Castilla-León Castilla-La Mancha Cataluña
## 2 2 3
## ComValenciana Extremadura Galicia
## 2 2 2
## Madrid Murcia Navarra
## 3 2 3
## País Vasco Rioja Ceuta
## 3 3 1
## Melilla
## 1
##
## Within cluster sum of squares by cluster:
## [1] 2.641013 27.709379 15.420216
## (between_SS / total_SS = 63.7 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss" "withinss"
## [5] "tot.withinss" "betweenss" "size" "iter"
## [9] "ifault"Podemos observar que en la salida de esta función tenemos información, entre otras cosas, sobre el conglomerado al que pertenece cada comunidad autónoma, que se puede extraer directamente utilizando $cluster (ver Available components)
km1$cluster ## Andalucía Aragón Asturias
## 2 3 2
## Baleares Canarias Cantabria
## 3 2 2
## Castilla-León Castilla-La Mancha Cataluña
## 2 2 3
## ComValenciana Extremadura Galicia
## 2 2 2
## Madrid Murcia Navarra
## 3 2 3
## País Vasco Rioja Ceuta
## 3 3 1
## Melilla
## 1Si además, la orden anterior se incluye dentro de la función sort aparecerán las comunidades autónomas ordenadas por conglomerado
sort(km1$cluster) ## Ceuta Melilla Andalucía
## 1 1 2
## Asturias Canarias Cantabria
## 2 2 2
## Castilla-León Castilla-La Mancha ComValenciana
## 2 2 2
## Extremadura Galicia Murcia
## 2 2 2
## Aragón Baleares Cataluña
## 3 3 3
## Madrid Navarra País Vasco
## 3 3 3
## Rioja
## 3Los conglomerados identificados son los mismos que los obtenidos en el análisis jerárquico (observe que el grupo 1 del jeráquico es el grupo 3 del no jerárquico). Se puede realizar una visualización de los grupos sobre el espacio de las dos primeras componentes principales:
fviz_cluster(km1, ccaa_tip, ellipse.type = "convex", palette = "rainbow_hcl")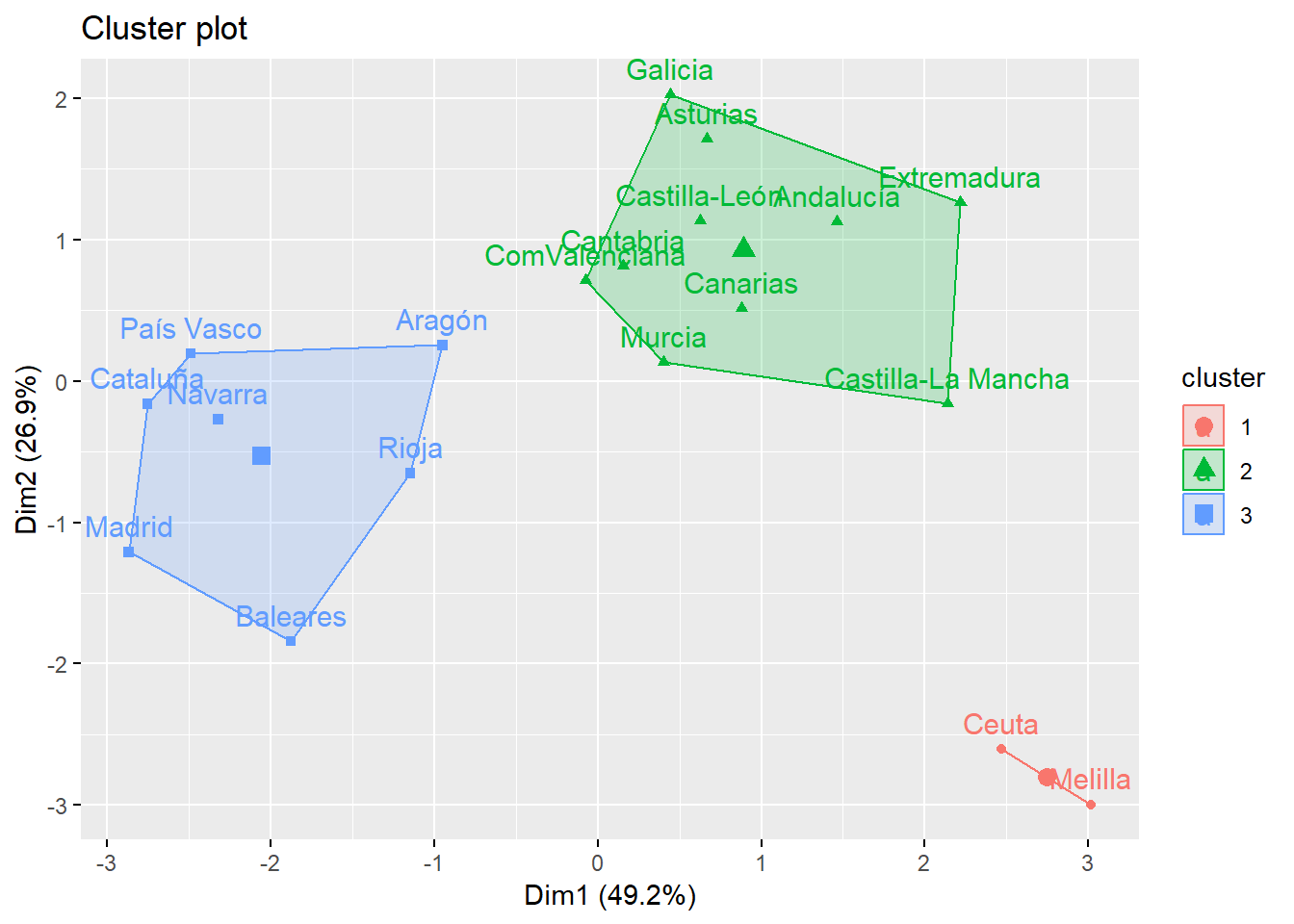
b) kmeans utilizando los centroides del análisis jerárquico como centro de inicio (no aleatorio).
Para poder utilizar como punto de partida en el método de kmeans, el resultado obtenido en el análisis jerárquico con hclust, necesitamos calcular y guardar en un objeto los centroides de los 3 grupos obtenidos.
Esto se puede hacer de varias formas, con la función cls.attrib del paquete clv,
library(clv) # Cálculos sobre los conglomerados
cent <- cls.attrib(ccaa_tip, sol)$cluster.center
colnames(cent) <- colnames(ccaa_tip)
cent## tasainm tasaem tasaact tasaemp tasaparo ipc
## c1 -0.45375230 -0.3051431 -0.4315810 -0.5666043 0.3739426 0.6001862
## c2 -0.04418771 -0.2840594 0.6480692 1.1183820 -0.8991167 -0.8183132
## c3 2.42341846 2.5199234 -0.1103369 -1.0813154 1.2771953 -0.1368348
## pibpc
## c1 -0.6229819
## c2 1.1374057
## c3 -0.8660104o programándolo nosotros mismos,
# data frame con los datos originales tipificados y el grupo al que pertenece cada comunidad autónoma
ccaa_tip.res <- as.data.frame(ccaa_tip)
ccaa_tip.res$conglomerado <- sol
# Cálculo de los centroides
centro <- NULL
centroides <- NULL
for (i in 1:3) {
centro <- apply(subset(ccaa_tip.res, conglomerado ==i, select = c(1:7)), 2, mean)
centroides <- rbind(centroides, centro)
}
rownames(centroides) <- paste("centro", 1:3, sep = " ")
head(centroides)## tasainm tasaem tasaact tasaemp tasaparo
## centro 1 -0.45375230 -0.3051431 -0.4315810 -0.5666043 0.3739426
## centro 2 -0.04418771 -0.2840594 0.6480692 1.1183820 -0.8991167
## centro 3 2.42341846 2.5199234 -0.1103369 -1.0813154 1.2771953
## ipc pibpc
## centro 1 0.6001862 -0.6229819
## centro 2 -0.8183132 1.1374057
## centro 3 -0.1368348 -0.8660104Los objetos cent y centroides contienen la misma información, los centroides de los tres grupos determinados en el análisis jerárquico y que utilizaremos como centros de inicio en el análisis no jerárquico k-means.
km2 <- kmeans(ccaa_tip, centers = cent)
sort(km2$cluster)## Andalucía Asturias Canarias
## 1 1 1
## Cantabria Castilla-León Castilla-La Mancha
## 1 1 1
## ComValenciana Extremadura Galicia
## 1 1 1
## Murcia Aragón Baleares
## 1 2 2
## Cataluña Madrid Navarra
## 2 2 2
## País Vasco Rioja Ceuta
## 2 2 3
## Melilla
## 3En este caso, coinciden tanto los conglomerados identificados como la denominación del grupo. La visualización de los grupos también se puede hacer gráficamente,
fviz_cluster(km2, ccaa_tip, ellipse.type = "convex", palette = "rainbow_hcl")Obsérvese que el objeto creado (km1 o km2) contiene información del tamaño y composición de los conglomerados ($size y $conglomerado), los centroides finales ($centers) y las sumas de cuadrados entre e intra conglomerados ($betweenss y $withinss).
Análisis de conglomerados utilizando FactoMineR
Otra forma de realizar un análisis de conglomerados es utilizando las funciones del paquete FactoMineR, e incluso la implementación de las mismas en forma de aplicación shiny con las funciones del paquete Factoshiny. Para utilizar dichas funciones debe instalar y cargar ambos paquetes.
library(FactoMineR)
library(Factoshiny)Comencemos por ver el uso de la función HCPC del paquete FactoMineR. Esta función realiza un análisis de conglomerados, a partir de los resultados de un análisis de componentes principales previo o de un data frame.
Vamos a realizar el análisis de conglomerados con la función HCPC a partir de los resultados obtenidos en el análisis de componentes principales con la función PCA del mismo paquete,
pca <- PCA(ccaa_tip, ncp = 7, graph = F)La función HCPC lleva a cabo un análisis de conglomerados jerárquico y lo refina con un kmeans (consol = TRUE). Como argumentos emplearemos la salida del análisis de componentes principales previo, el método de agrupación method=complete y la opción nb.clust = -1 para que sea la propia función la que decida el número de conglomerados óptimo,
conglom <- HCPC(pca, nb.clust = -1, method="complete", consol = TRUE)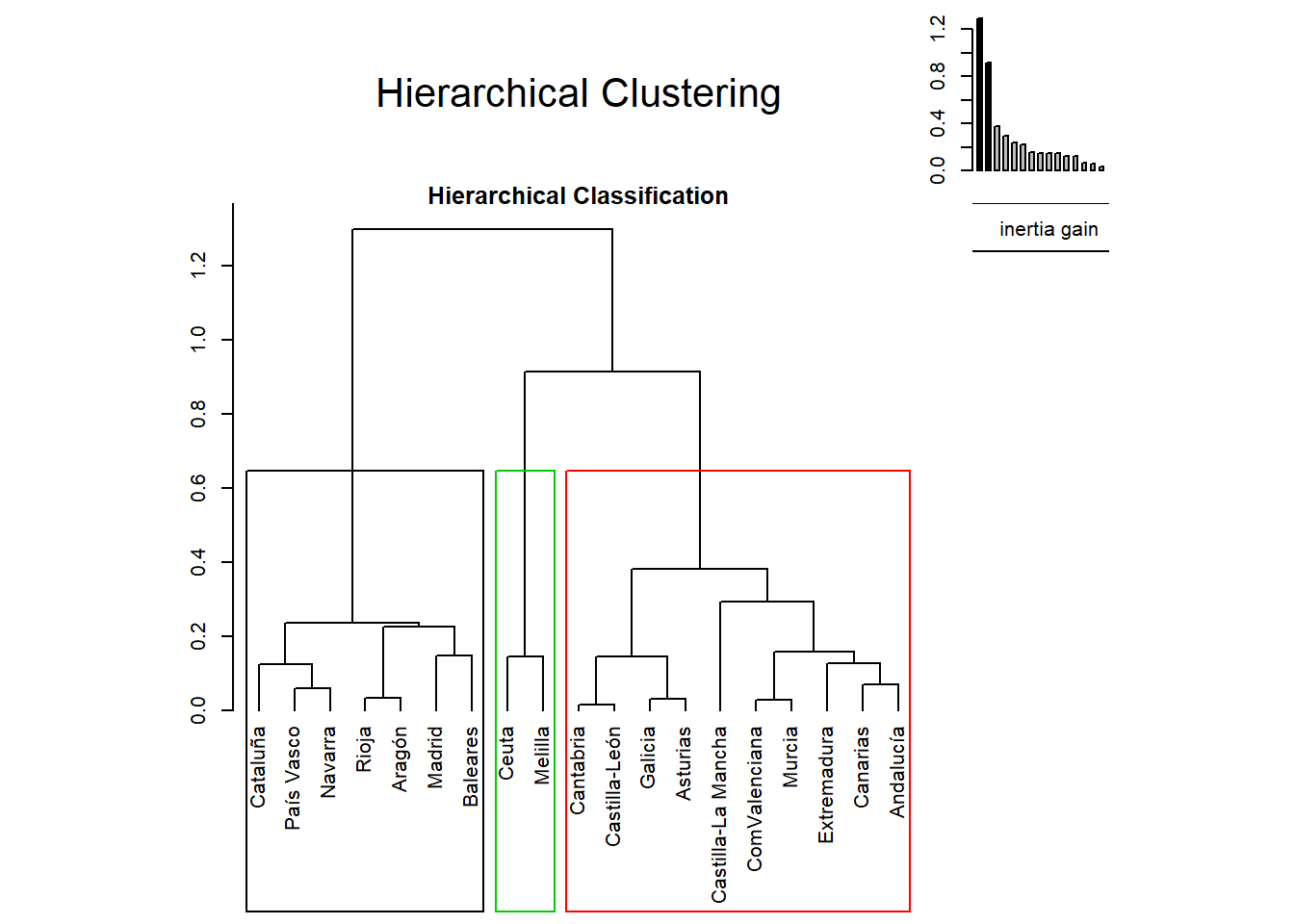
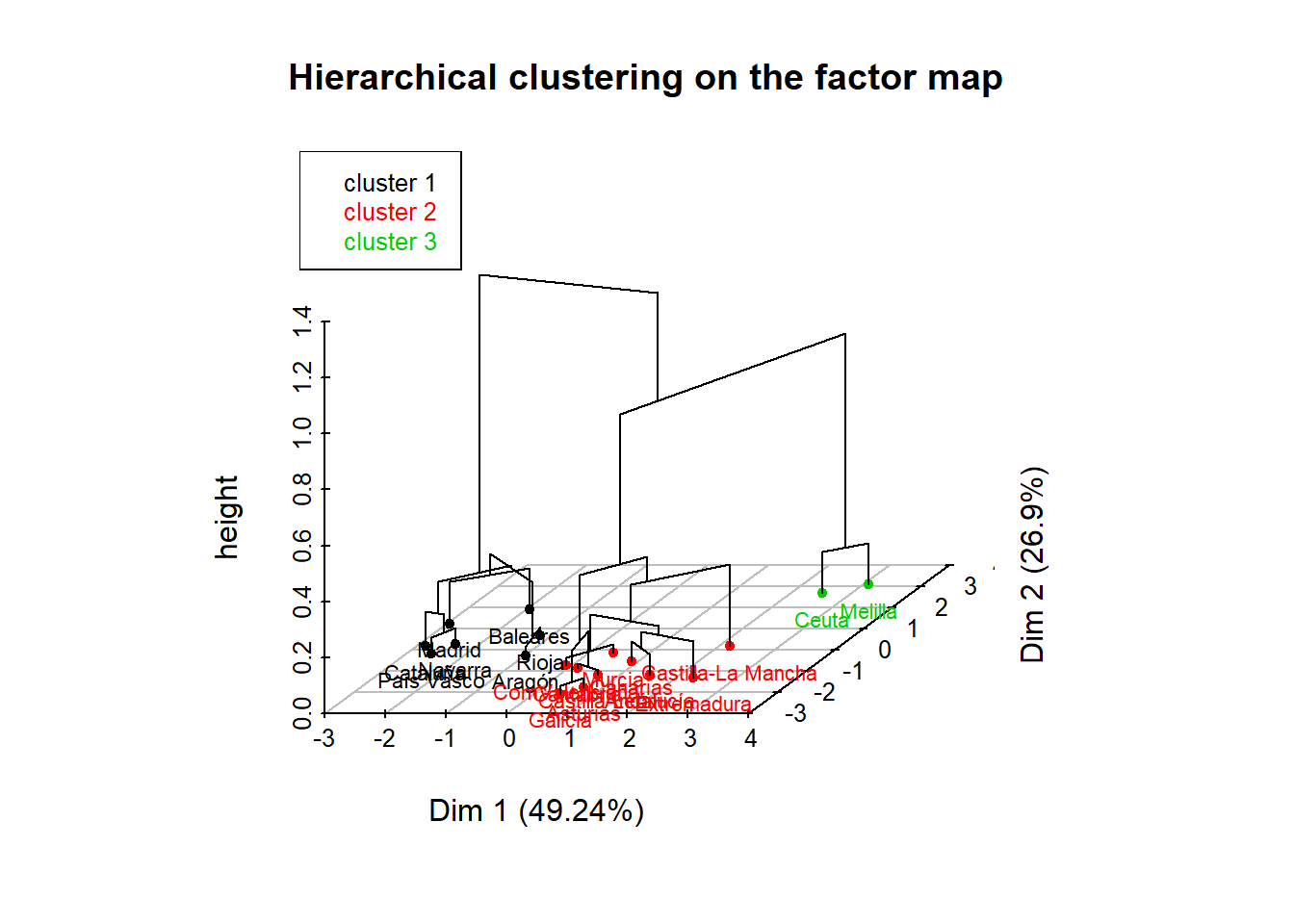
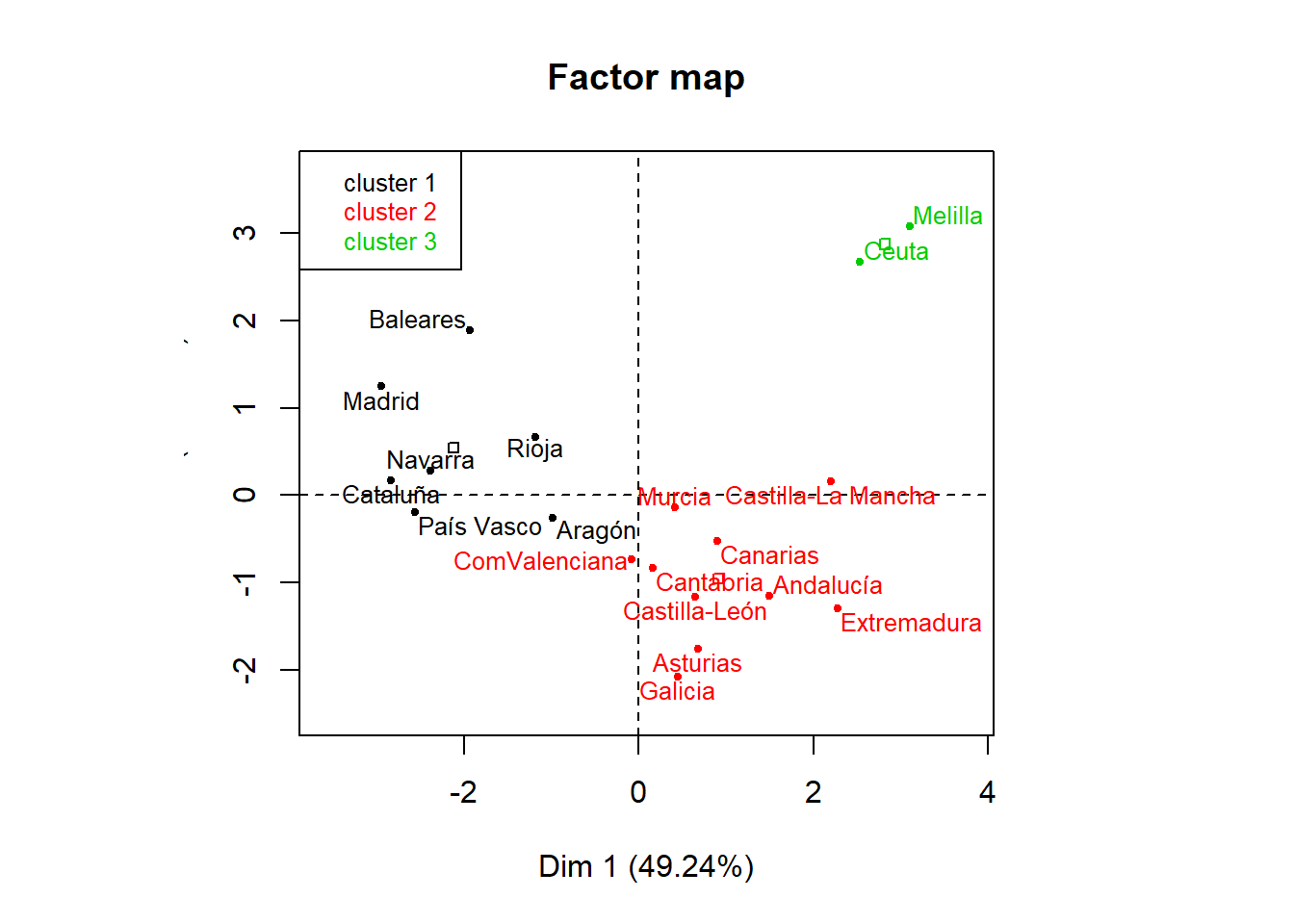
El objeto conglom contiene, entre otros elementos, el data frame conglom$data.clust que incluye en la columna clust la información sobre el grupo al que pertenece cada comunidad autónoma, que puede ser extraída, para su presentación de forma ordenada por conglomerado, con las siguientes órdenes
for (i in 1:3) {
print(paste("Conglomerado ", i, ": ", sep = ""), quote = F)
print(rownames(subset(conglom$data.clust, conglom$data.clust$clust==i)), quote = F)
}## [1] Conglomerado 1:
## [1] Aragón Baleares Cataluña Madrid Navarra País Vasco
## [7] Rioja
## [1] Conglomerado 2:
## [1] Andalucía Asturias Canarias
## [4] Cantabria Castilla-León Castilla-La Mancha
## [7] ComValenciana Extremadura Galicia
## [10] Murcia
## [1] Conglomerado 3:
## [1] Ceuta MelillaSe observa que los resultados obtenidos utilizando como input las componentes principales coincide con el análisis realizado directamente con la matriz de distancia de las variables originales tipificadas (ver epígrafe Conglomerado Jerárquico con hclust, metodo complete). Esto pone de manifiesto que las correlaciones detectadas entre las variables originales no son suficientemente grandes para influir en la matriz de distancia, con lo que no sería necesario hacer un análisis de componentes principales previo.
En el paquete Factoshiny se encuentran implementadas algunas aplicaciones shiny que facilitan el uso de las funciones del paquete FactoMineR. La función a utilizar para acceder a la aplicación shiny para realizar un análisis de conglomerados es HCPCshiny. Su uso abre la aplicación en formato web, estando activa para trabajar mientras el usuario lo desee. La forma de acceder a la misma es:
HCPCshiny(pca)El código anterior tiene como resultado que se abra la siguiente página, desde la que puede interactuar, en su navegador:
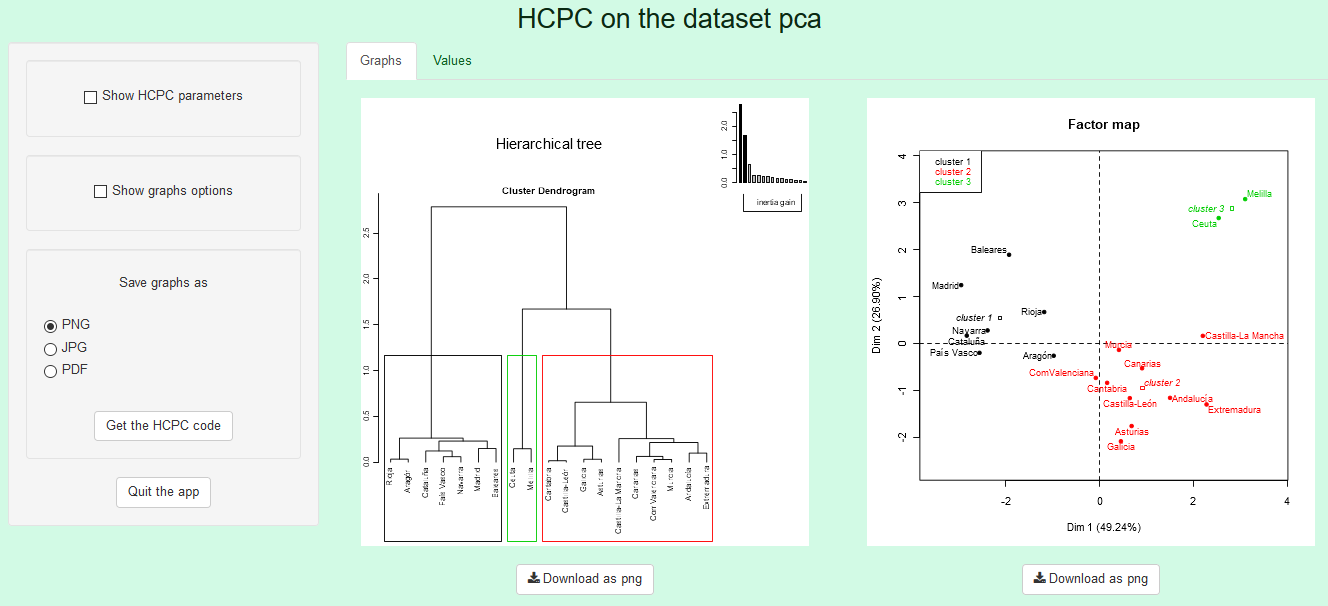
Etapa 5. Interpretación de los conglomerados
Para interpretar los conglomerados, recurrimos a:
- Los diagramas de caja de las variables de interés por conglomerado,
par(mfrow = c(1, 2))
boxplot(tasainm ~ conglomerado, data = resccaa, main = "Tasa inmigración")
abline(h = mean(ccaa$tasainm), col = "red", lty = 2)
boxplot(tasaem ~ conglomerado, data = resccaa, main = "Tasa emigración")
abline(h = mean(ccaa$tasaem), col = "red", lty = 2)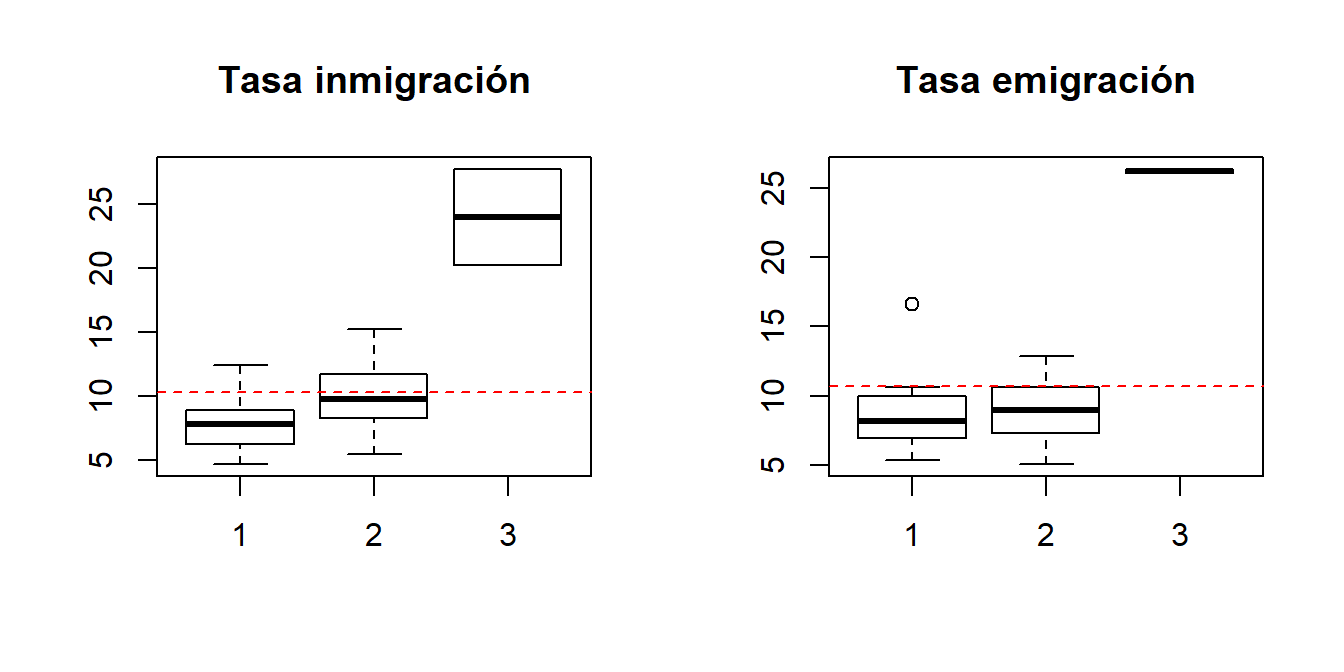
par(mfrow = c(1, 3))
boxplot(tasaact ~ conglomerado, data = resccaa, main = "Tasa de actividad")
abline(h = mean(ccaa$tasaact), col = "red", lty = 2)
boxplot(tasaemp ~ conglomerado, data = resccaa, main = "Tasa empleo")
abline(h = mean(ccaa$tasaemp), col = "red", lty = 2)
boxplot(tasaparo ~ conglomerado, data = resccaa, main = "Tasa de paro")
abline(h = mean(ccaa$tasaparo), col = "red", lty = 2)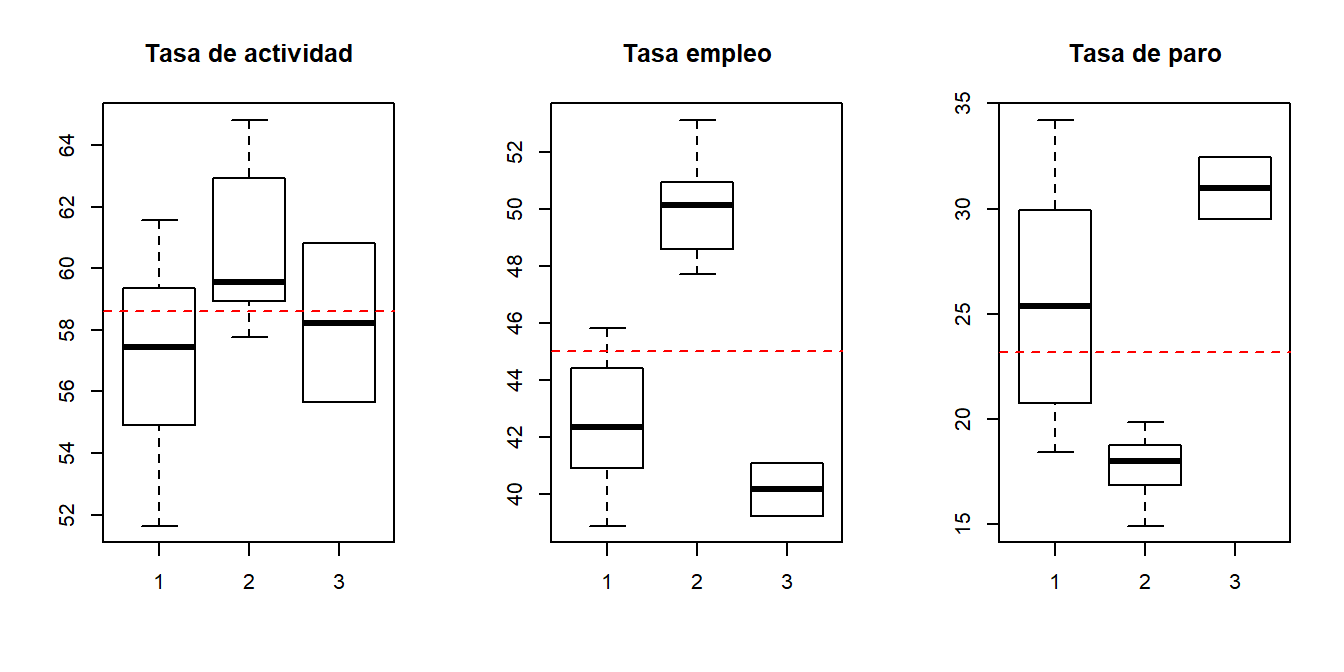
par(mfrow = c(1, 2))
boxplot(ipc ~ conglomerado, data = resccaa, main = "IPC")
abline(h = mean(ccaa$ipc), col = "red", lty = 2)
boxplot(pibpc ~ conglomerado, data = resccaa, main = "PIBpc")
abline(h = mean(ccaa$pibpc), col = "red", lty = 2)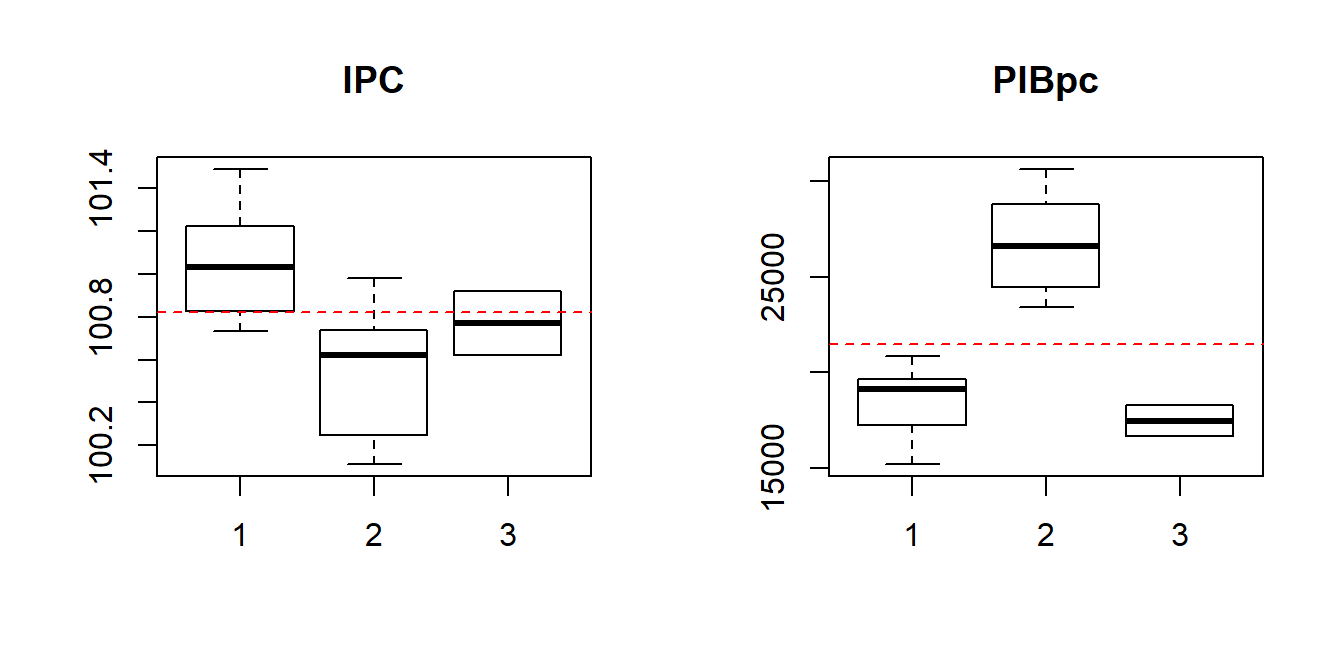
- El vector de medias de las variables tipificadas en cada grupo (centroide) y su representación gráfica utilizando la función
parcoorddel paqueteMASS,
cent## tasainm tasaem tasaact tasaemp tasaparo ipc
## c1 -0.45375230 -0.3051431 -0.4315810 -0.5666043 0.3739426 0.6001862
## c2 -0.04418771 -0.2840594 0.6480692 1.1183820 -0.8991167 -0.8183132
## c3 2.42341846 2.5199234 -0.1103369 -1.0813154 1.2771953 -0.1368348
## pibpc
## c1 -0.6229819
## c2 1.1374057
## c3 -0.8660104library(MASS)
parcoord(km2$centers , col = rainbow_hcl(k), var.label = T, lwd = 2)
legend("left", lwd = 2, col = rainbow_hcl(k),
legend = c("Clúster1", "Clúster2", "Clúster3"))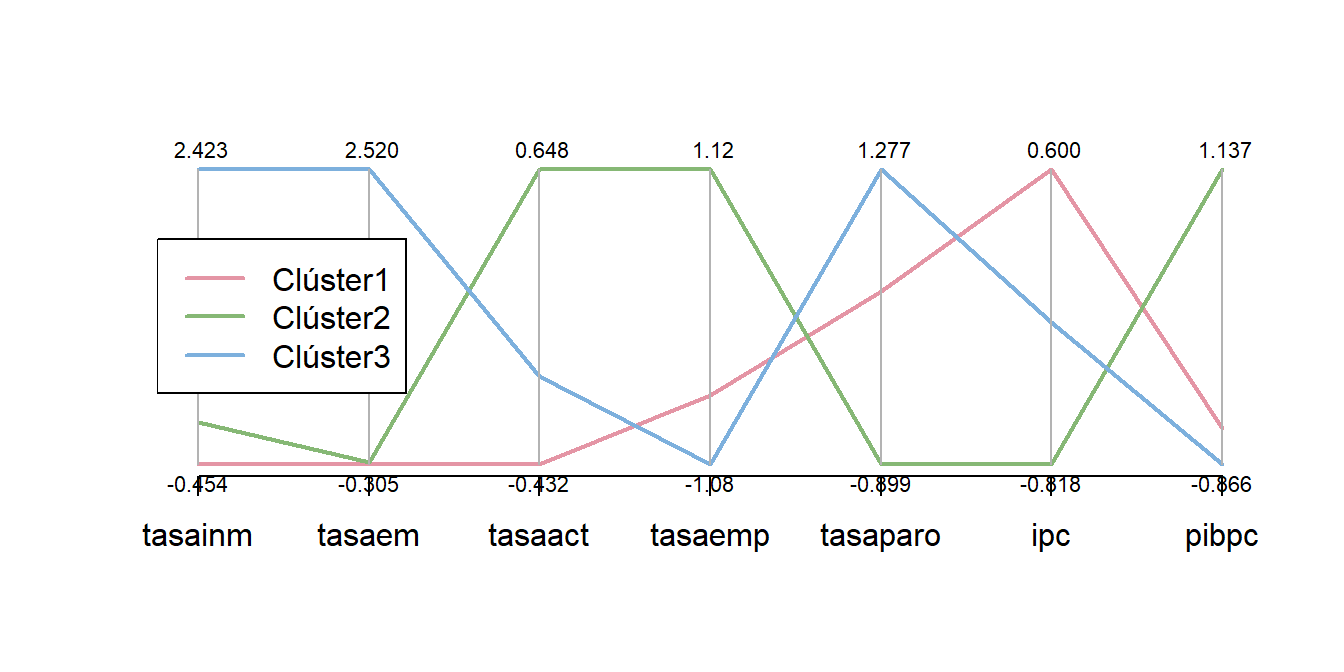
En los gráficos anteriores podemos observar que:
El grupo 1 (Andalucía, Asturias, Canarias, Cantabria, Castilla-León, Castilla-La Mancha, Comunidad Valenciana, Extremadura, Galicia y Murcia) tiene los valores más altos del IPC (casi todas por encima de la media). Además, presentan valores más bajos en la tasa de actividad que el grupo 2 y semejantes a los del grupo 3, pero con una varibilidad o dispersión superior. En las tasas empleo y de paro, los valores están entre los de los grupos 2 y 3, tomando en el primer indicador valores por debajo de la media. El grupo 1 muestra mucha dispersión en el indicador tasa de paro (en general, por encima de la media). En cuanto a las tasas de inmigración e emigración son bajas y similares a las del grupo 2, aunque ligeramente inferiores. El PIBpc presenta valores inferiores a la media y con mayor dispersión que en el grupo 2. Como puede verse la variabilidad dentro del grupo 1 en algunas variables podría justificar su división en subgrupos. De hecho, si se repitiera el análisis considerando 4 conglomerados, el nuevo grupo surgiría de la escisión del grupo 1, separando las comunidades del norte de las comunidades del sur.
Las comunidades autónomas del grupo 2 (Madrid, Cataluña, País Vasco, Navarra, La Rioja, Aragón y Baleares) tienen los valores más altos en las tasas empleo y en el PIB per cápita, así como los valores más bajos en la tasa de paro, siendo estos indicadores los que caracterizan principalmente a este grupo. Además, aunque tienen valores bajos en tasas de inmigración y emigración, la mayoría por debajo de la media, éstos son ligeramente superiores a los del grupo 1.
Las ciudades autónomas del grupo 3 (Ceuta y Melilla) tienen valores más altos en las tasas de inmigración y emigración que las comunidades de los grupos 1 y 2, mostrando un comportamiento diferencial en estos indicadores, tal y como se indicó al principio de este estudio. Además, también presentan los valores más bajos en tasa de empleo (por debajo de la media) y más altos en la tasa de paro (por encima de la media).
Puede explorar la varibilidad entre y dentro de los grupos con la función cls.scatt.data del paquete clv,
cls.scatt.data(ccaa_tip, sol)$intracls.complete # dentro del grupo## c1 c2 c3
## [1,] 3.701129 2.917976 2.298266cls.scatt.data(ccaa_tip, sol)$intercls.complete # entre grupos## c1 c2 c3
## c1 0.000000 5.839718 5.736633
## c2 5.839718 0.000000 6.835635
## c3 5.736633 6.835635 0.000000El conglomerado menos homogéneo de los tres es el grupo 1 formado por 10 comunidades autónomas y el grupo 2 es el que más distanciado está de los otros grupos.
Aplicación interactiva (métodos de agrupación)
Si desea seguir explorando otros métodos de agrupación, o la composición de los conglomerados en caso de considerar un número diferente a tres, puede utilizar la siguiente aplicación:
Opcional / Avanzado
Forma alternativa de obtener el gráfico de sedimentación (gráfico de codo)
wss <- (nrow(ccaa_tip)-1)*sum(apply(ccaa_tip,2,var))
for (i in 2:10) wss[i] <- sum(kmeans(ccaa_tip, centers = i)$withinss)
plot(1:10, wss, type = "b", xlab = "Número de conglomerados", ylab = "Variabilidad dentro del grupo" )Formas alternativas de obtener el centroide de un conglomerado
A continuación mostramos algunos métodos alternativos para el cálculo de los centroides:
- Con el paquete
dplyr:
ccaa_tip.res <- as.data.frame(ccaa_tip)
ccaa_tip.res$conglomerado <- (sol)
library(dplyr)
cent <- ccaa_tip.res%>%
group_by(conglomerado)%>%
summarise(tasainm = mean(tasainm), tasaem = mean(tasaem), tasaact = mean(tasaact), tasaemp = mean(tasaemp), tasaparo = mean(tasaparo), ipc = mean(ipc), pibpc = mean(pibpc))
cent <- as.data.frame(cent[2:8])
cent## tasainm tasaem tasaact tasaemp tasaparo ipc
## 1 -0.45375230 -0.3051431 -0.4315810 -0.5666043 0.3739426 0.6001862
## 2 -0.04418771 -0.2840594 0.6480692 1.1183820 -0.8991167 -0.8183132
## 3 2.42341846 2.5199234 -0.1103369 -1.0813154 1.2771953 -0.1368348
## pibpc
## 1 -0.6229819
## 2 1.1374057
## 3 -0.8660104- Usando la función
aggregate:
aggregate(ccaa_tip.res, by = list(conglomerado = ccaa_tip.res$conglomerado), mean)## conglomerado tasainm tasaem tasaact tasaemp tasaparo
## 1 1 -0.45375230 -0.3051431 -0.4315810 -0.5666043 0.3739426
## 2 2 -0.04418771 -0.2840594 0.6480692 1.1183820 -0.8991167
## 3 3 2.42341846 2.5199234 -0.1103369 -1.0813154 1.2771953
## ipc pibpc conglomerado
## 1 0.6001862 -0.6229819 1
## 2 -0.8183132 1.1374057 2
## 3 -0.1368348 -0.8660104 3
Grupo Innovación Docente: Estadística en Ciencias Sociales. Universidad de Murcia.
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.