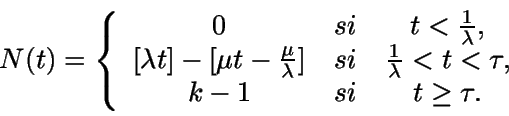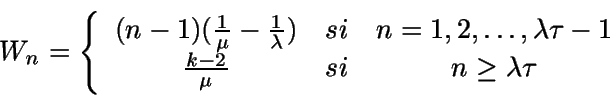Siguiente: Introducción a los procesos estocásticos
Nivel anterior: Ampliación Modelos I.O.
Previa: Objetivos
En el modelo determinístico los tiempos de servicio son conocidos
con exactitud (no son aleatorios). Con la notación que se
introdujo anteriormente, se estudiará el modelo D/D/1/k-1, donde:
-
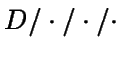 significa que el tiempo entre llegadas es
constantemente igual a
significa que el tiempo entre llegadas es
constantemente igual a
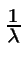 ,
,
 .
(Luego
.
(Luego 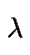 denota el número de llegadas por unidad de
tiempo, llamado tasa de llegadas)
denota el número de llegadas por unidad de
tiempo, llamado tasa de llegadas)
-
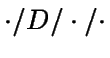 significa que el tiempo de servicio es
constantemente igual a
significa que el tiempo de servicio es
constantemente igual a
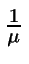 ,
,
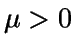 ,
de donde
,
de donde
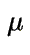 es el número de servicios por unidad de tiempo en período de
ocupación, llamado tasa de servicio.
es el número de servicios por unidad de tiempo en período de
ocupación, llamado tasa de servicio.
-
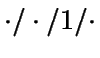 indica que hay un servidor.
indica que hay un servidor.
-
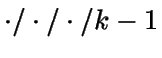 es la capacidad del sistema, el número máximo de
clientes que admite el sistema. Cuando un cliente está en el
servicio sólo puede haber k-2 clientes en cola, y el k-ésimo
cliente que aspire a entrar en el sistema es rechazado.
es la capacidad del sistema, el número máximo de
clientes que admite el sistema. Cuando un cliente está en el
servicio sólo puede haber k-2 clientes en cola, y el k-ésimo
cliente que aspire a entrar en el sistema es rechazado.
Observación: Salvo que se diga lo contrario, de aquí en adelante se
supondrá
 ,
pues en caso
contrario todo cliente puede ser servido sin problema y no se
produce el fenómeno de cola.
,
pues en caso
contrario todo cliente puede ser servido sin problema y no se
produce el fenómeno de cola.
Interesa conocer el estado del sistema en el instante t, es
decir, conocer N(t) y L(t) y los tiempos que afectan al
cliente n, es decir, Wn y 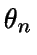 .
.
N(t) denota el número de clientes en el sistema, es decir, el
número de clientes en cola más el número de clientes que están
siendo servidos en el instante t.
Suponemos que en t=0 no hay clientes (N(0)=0).
Definimos 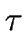 como el instante de tiempo en el que se produce
el primer rechazo, es decir, llega un cliente cuando en el sistema
ya hay k-1 clientes.
como el instante de tiempo en el que se produce
el primer rechazo, es decir, llega un cliente cuando en el sistema
ya hay k-1 clientes.
Si
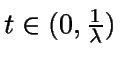 ,
no ha llegado todavía ningún
cliente, por lo que en este intervalo de tiempo no hay clientes en
el sistema.
,
no ha llegado todavía ningún
cliente, por lo que en este intervalo de tiempo no hay clientes en
el sistema.
Si
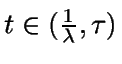 ,
entonces N(t) es igual al
número de llegadas menos el número de salidas hasta t, donde
,
entonces N(t) es igual al
número de llegadas menos el número de salidas hasta t, donde
"nº de llegadas hasta t" =
![$[\frac{t}{\frac{1}{\lambda}}]=[\lambda t]$](img27.gif) .
.
"nº de salidas hasta t" =
![$[\frac{t-\frac{1}{\lambda}}{\frac{1}{\mu}}]=[ \mu
t-\frac{\mu}{\lambda}]$](img28.gif) .
.
Por lo tanto
![$N(t)=[\lambda t]-[ \mu t-\frac{\mu}{\lambda}]$](img29.gif) .
.
Para 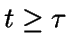 ,
vamos a restringirnos al caso más
sencillo: el tiempo de servicio es un múltiplo entero del tiempo
entre llegadas, es decir,
,
vamos a restringirnos al caso más
sencillo: el tiempo de servicio es un múltiplo entero del tiempo
entre llegadas, es decir,
En este caso, siempre que se produce la salida de un cliente hay una
llegada simultánea. Así, no puede suceder que haya simultáneamente una salida
y un rechazo, pues si un cliente sale, se deja una plaza libre en
el sistema para el otro cliente que llega en ese momento. En
consecuencia, el número de clientes es creciente hasta que a
partir del instante 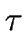 es constantemente igual a la capacidad
del sistema, k-1. Por lo tanto, se tiene
es constantemente igual a la capacidad
del sistema, k-1. Por lo tanto, se tiene
Suponiendo que se tiene disciplina FIFO, vamos a definir los
valores asociados a cada cliente.
Wn= es el tiempo de espera en cola del cliente n-ésimo.
Sn= es el tiempo del n-ésimo servicio.
Tn= es el tiempo entre la n-ésima y la (n+1)-ésima llegada aceptadas.
Expresemos Wn+1 en función de Wn, Sn y Tn.
Si
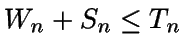 entonces
Wn+1=0.
entonces
Wn+1=0.
Si
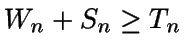 entonces
Wn+1=Wn+Sn-Tn.
entonces
Wn+1=Wn+Sn-Tn.
Aunque esto es cierto en general, en el caso del sistema que estamos
estudiando, si 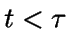 ,
entonces
,
entonces
por lo que
Si 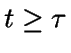 ,
entonces cualquier cliente que sea aceptado será
servido después de que hayan sido atendidos los k-2 que le
preceden (y no los k-1, pues su llegada ha coincidido con una
salida). Así
,
entonces cualquier cliente que sea aceptado será
servido después de que hayan sido atendidos los k-2 que le
preceden (y no los k-1, pues su llegada ha coincidido con una
salida). Así
En resumen: